Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.3 - Ex. 4
No divisor de tensão mostrado, a potência entregue pela fonte é de 8mW e . Encontre .
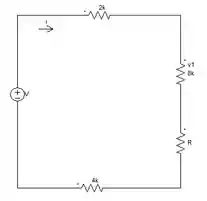
Passo 1
O exercício quer que encontremos a as tensões dos resistores, o valor de R e a corrente que está circulando no circuito em série.
Como foi dado o valor da tensão do resistor de 8kΩ, vamos descobrir o , usando a relação .
Agora ficou fácil encontrar o né???!!!! Como todos os resistores estão em série a soma deles resulta no Vamos colocar todos os valores dos resistores que temos na equação:
Passo 2
Agora, vamos descobrir o (o valor da tensão total do circuito, que está sendo representada pela fonte) usando a potência e o . Temos que usar uma nova fórmula para potência:
A potência da fonte nos foi dado, que é 8mW e o = 32k. Vamos substituir os valores:
Olha só! Já descobrimos o e como diz a relação , então vamos substituir:
.
Passo 3
Agora falta pouco! Falta encontrarmos a corrente do circuito. Para isso precisamos usar o valor da fonte e a soma de todos os resistores Se temos tensão e resistor, vamos utilizar a lei de Ohm!