Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 62

Considere o circuito da figura 6.84. Dado que v t = 12 e - 3 t   m V para t > 0 e i 1 0 = - 10 m A , determine:

a i 2 0 ;

b i 1 t   e   i 2 t .

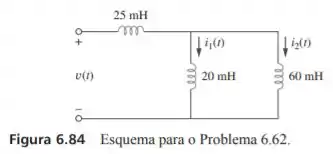
Passo 1

Primeiramente vamos encontrar a indutância equivalente que será dada pela associação em paralelo dos indutores de 20 e 60, juntamente com a associação em série com o indutor de 25, lembrando-se que para indutores procede-se como se fosse para resistores. Assim, teremos

L e q = 25 + 20 ⋅ 60 20 + 60 = 40   m H

Da equação do indutor temos

v = L e q ⋅ d i d t →

i = 1 L e q ⋅ ∫ v t d t + i 0 = 10 - 3 40 ⋅ 10 - 3 ⋅ ∫ 0 t 12 ⋅ e - 3 t   d t + i 0 = - 0.1 ⋅ e - 3 t - 1 + i ( 0 )

Aplicando o divisor de corrente e o fato que todas as correntes eram zero quando o circuito é ligado

i 1 = 60 80 ⋅ i = 3 4 ⋅ i   ,     i 1 = 1 4 ⋅ i

i 1 0 = 3 4 ⋅ i 0 → 0.75 ⋅ i 0 = - 0.01 → i 0 = - 0.0133

Dessa forma, teremos

i 2 = 1 4 ⋅ - 0.1 e - 3 t + 0.08667 = - 25 e - 3 t + 21.67   m A

→ i 2 0 = - 25 + 21.67 =   - 3.33   m A

Passo 2

Por fim, vamos ter

i 1 = 3 4 ⋅ - 0.1 e - 3 t + 0.08667 = - 75 e - 3 t + 65   m A

i 2 =   - 25 e - 3 t + 21.67   m A

Resposta

a   i 2 0 = - 3.33   m A

b   i 1 = - 75 e - 3 t + 65   m A ,     i 2 = - 25 e - 3 t + 21.67   m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um indutor de 5 H muda sua corrente de 3 A em 0,2 s. A tensão produzida nos terminais do indutor é:75 V8,888 V3 V 1,2 V
Para o circuito mostrado em (a), a fonte de tensão é dada em (b). calcule a corrente i em i l 0 = - 1 A para:a) 0t1 s b) 1t2 s
No Problema 6.3, suponha que o valor da tensãono indutor em t = 0 seja -18 V em vez de 3 V.a) Determine as expressões numéricas para i e v em t $ 0.b) Especifique os intervalos de tempo em que o indut
A corrente em um indutor de 200 mH é i = (B1 cos 200t + B2 sen 200t)e-50t A, t $ 0. A tensão no indutor (convenção passiva) é 4,25 V em t = 0. Calcule a potência nos terminais do indutor em t = 25 ms.