Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 46
Determine e a energia armazenada no capacitor e indutor no circuito da figura 6.69 em condições de CC.
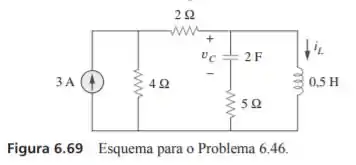
Passo 1
Em condições de corrente contínua devemos calcular o valor de dados no circuito da imagem, além da energia armazenada no capacitor e no indutor. Para análise do nosso circuito podemos redesenhá-lo da seguinte forma para atender as condições pedidas pelo enunciado
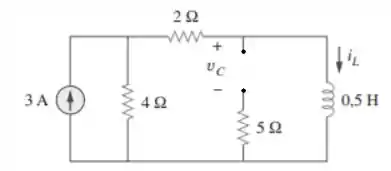
Aplicando o divisor de corrente nós temos que
Além disso, vamos ter
Passo 2
Para calcularmos a energia armazenada no capacitor e no indutor, respectivamente, vamos utilizar as seguintes fórmulas
Substituindo os valores encontrados acima e os fornecidos no circuito vamos encontrar
Resposta
Exercícios de Livros Relacionados
a Para dois indutores em série como aqueles mostrados na figura 6.81ª, demonstre que o princípio da divisão da tensão é v 1 = L 1 L 1 + L 2 ⋅ v s ,v 2 = L 2 L 1 + L 2 ⋅ v S Supondo que as condições in
Determine a L e q que pode ser usada para representar o circuito indutivo da figura 6.79 nos terminais.
No circuito da figura 6.85, esboce v 0 .
Considere o circuito da figura 6.83. Determine: aL e q ,i 1 tei 2 t , se i s = 3 e - tm A ; b v 0 t ; c a energia armazenada no indutor de 20m H em t = 1 s .
Determine a L e q em cada um dos circuitos da figura 6.78.