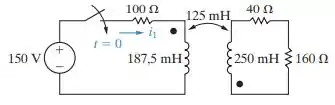
Não há nenhuma energia armazenada no circuito da Figura P13.36 no instante em que a chave é fechada. a) Determine I1. b) Use os teoremas dos valores inicial e final para determinar i 1(0+) e i 1(q). c) Determine i 1.
Passo 1
Falaaa, pessoal! Como vocês estão? Bora pra mais uma questão! No item a), o circuito no domínio do tempo fica:
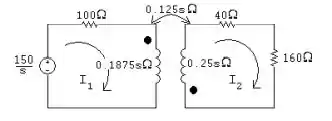
Logo,
Passo 2
No item b), já conseguimos pegar os valores para Vo.
Com o limite para s tendendo a 0.
E claro, ao infinito fica 0 porque o circuito abre.
Passo 3
Agora no item c, pra gente pegar a equação da corrente no item, temos;
Resposta
Resposta nos itens