Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 46
Considere o circuito ilustrado na Figura e determine:
- A função de transferência
- A amplitude de em
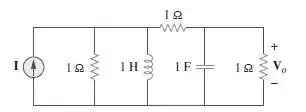
Passo 1
Pessoal, a primeira coisa que a gente pode fazer é encontrar a impedância equivalente entre o resistor de e o indutor de . Assim,
Agora vamos pegar essa fonte de corrente que está em paralelo com e vamos transformá-la em uma fonte de tensão em série com esse . O valor da fonte de tensão será:
Passo 2
Bom, na letra (a) queremos a função de transferência . Aplicando o divisor de tensão,
Passo 3
Agora, na letra (b), queremos saber a amplitude de quando . Assim,
Assim,
Resposta
Exercícios de Livros Relacionados
A chave no circuito da Figura P13.15 esteve fechada por um longo tempo antes de abrir em t = 0. a) Construa o circuito no domínio da frequência, para t0. b) Determine I 0 . c) Determine i 0 tp a r at
Um resistor de 200 V está em série com um capacitor de 62,5 mF. Essa combinação em série está em paralelo com um indutor de 400 mH. a) Expresse a impedância equivalente desses ramos paralelos no domín
Não há nenhuma energia armazenada no circuito da Figura P13.20, no instante em que a fonte de tensão é ligada e vg = 325u(t) V. a) Determine Vo e Io. b) Determine vo e i o. c) As soluções para vo e i
Não há nenhuma energia armazenada no circuito da Figura P13.21, no instante em que as fontes são conectadas. a) Determine I 1 seI 2 ( s ) . b) Use os teoremas do valor inicial e final para verificar o
Verifique se a solução das equações 13.91 e 13.92 para V2 resulta na mesma expressão que a da Equação 13.90