Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 65
Considere a Figura 10.108 e elabore um problema para ajudar outros estudantes a entender melhor o teorema de Norton.
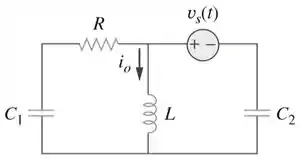
Passo 1
Vamos lá galera! O papel se inverteu novamente han? Mas sem problemas! As vantagens desse tipo de problema é que montando um problema, nós nos aperfeiçoamos mais ainda para explicar e solucionar o problema! Então chega de enrolação e vamos pra cima! O problema é o seguinte: “Ache na figura abaixo usando o teorema de Norton”
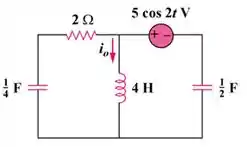
Passo 2
Para resolver essa questão, vamos primeiro transformar esse circuito para o domínio da frequência! Para achar o , vamos considerar o circuito abaixo:
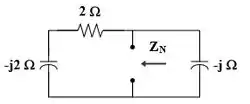
Passo 3
Fácil né? Agora vamos achar a corrente de norton!
Passo 4
Usando a divisão de corrente, temos que:
Resposta
Exercícios de Livros Relacionados
Para o circuito fasorial correspondente, substitua tudo à esquerda dos terminais a - b por seu equivalente Thévenin e use o resultado para calcular a resposta forçada i .
No circuito fasorial do Ex. 14.3.2, com i g 2 = 0 , e v g 1 permanecendo inalterado, substitua tudo, exceto o capacitor, por seu equivalente de Thévenin e use o resultado para calcular V ( s ) , o fas
Resolva o Prob. 16.6 usando análise nodal, como descrito no Prob. 16.18.
10.30) Para o circuito fasorial correspondente ao Ex. 11.2.3, substitua tudo, exceto o resistor de 2-Ω entre os terminais c-d pelo seu equivalente de Thévenin e calcule a corrente i em regime permanen
10.31) Para o circuito fasorial correspondente ao Ex. 11.2.3, substitua tudo à esquerda dos terminais a-b pelo seu equivalente de Norton e calcule a corrente i em regime permanente.