Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.3 - Ex. 4

No circuito fasorial do Ex. 14.3.2, com , e permanecendo inalterado, substitua tudo, exceto o capacitor, por seu equivalente de Thévenin e use o resultado para calcular , o fasor de . Note que o resultado conduz ao primeiro componente de da do no Ex. 14.3.2.

Passo 1

Queeee!!!!!!!!!

Bom... calma, calma. Vamos devagarzinho e desenrolar essa questão.

Temos o seguinte circuito:

Passo 2

Também sabemos que, para uma resistência , a impedância é:

Para uma indutância , sua impedância é:

E, para uma capacitância , sua impedância é:

Nesse sentido, para o circuito desse exercício, temos:

Passo 3

Vamos primeiro descobrir a impedância de Thévenin nos terminais do capacitor. Para isso, temos:

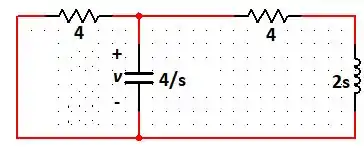
Dividindo a equação por e colocando em evidência, temos:

Passo 4

Para a tensão de Thévenin, a qual:

Temos que a tensão vista nos terminais do capacitor é dada por:

Simplificando a equação, temos:

Belezinha?? Massa né ;)

Resposta

Exercícios de Livros Relacionados

56.Para cada um dos circuitos da figura 10.99 determine os circuitos equivalentes de T h é v e n i n é e N o r t o n nos terminais a - b .

57. Usando a figura 10.100 elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos equivalentes de T h é v e n i n é e N o r t o n :

Usando o teorema de Thévenin, determine vo no circuito da Figura 10.105.

Considere a Figura 10.108 e elabore um problema para ajudar outros estudantes a entender melhor o teorema de Norton.

Nos terminais a-b, obtenha os circuitos equivalentes de Thévenin e de Norton para o circuito representado na Figura 10.109. Suponha ω = 10r a d / s .