Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 67
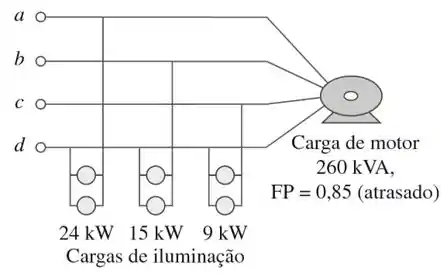
Conforme indicado na Figura 12.72, uma linha trifásica quadrifilar com tensão de fase igual a 120 V RMS e sequência de fase positiva alimenta uma carga de motor equilibrada a 260 kVA com FP = 0,85 (atrasado). A carga do motor está conectada a três linhas principais indicadas por a, b e c. Além disso, lâmpadas incandescentes (FP unitário) são ligadas como segue: 24 kW da linha c para o neutro, 15 kW da linha b para o neutro e 9 kW da linha c para o neutro.*
- Se forem dispostos três wattímetros para medir a potência em cada linha, calcule a leitura de cada medidor.
- Determine a magnitude da corrente na linha do neutro.
Passo 1
Para calcularmos a potencia de cada wattimetro, temos que a potencia para o motor, é:
O motor alimentado pro fase é:
Mas lembrando que o wattimetro é a potencia de TODA a linha, então somemos as cargas de ilumminação!
Passo 2
Como a carga é balanceada, significa que
Logo,
Passo 3
Se tratarmos comos essas ondas sendo defasadas -120 graus cada, entao: