Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 76
Considere a Figura e elabore um problema para ajudar outras estudantes a entender melhor como funciona um transformador trifásico e a conexão estrela-triângulo.
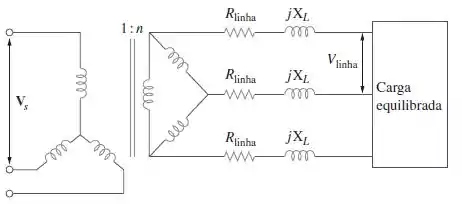
Passo 1
Pessoal, vamos resolver a seguinte questão:
“Um transformador trifásico com ligação está conectado a uma carga de com fator de potência (adiantado) através do alimentador que tem impedância por fase. Seja e . Encontre a magnitude:
- Da corrente de linha na carga
- Da tensão de linha no secundário do transformador
- Da corrente de linha no primário do transformador”
Vamos lá, galera, para a letra (a)! Na carga, temos que:
A tensão de fase pode ser calculada através da equação:
A potência aparente pode ser calculada como:
A partir dessa equação, nós podemos calcular a corrente de linha na carga!
Passo 2
Na letra (b), queremos a tensão de linha no secundário do transformador. Seja .
A corrente é igual a:
Assim, a tensão de linha do secundário é igual a:
Passo 3
Por fim, na letra (c), queremos a corrente de linha no primário do transformador. Para conexões :
Assim, a corrente é igual a: