Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 48

Considere a Figure 13.113 e elabore um problema para ajudar outros estudantes a entender melhor como funciona os transformadores ideais.

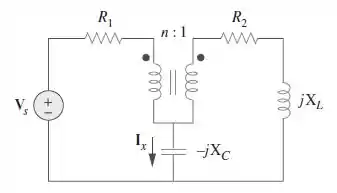
Passo 1

Galera, vamos resolver a seguinte questão:

“Para o circuito dado, obter a corrente I x . Assuma que R 1 = 4   Ω ,   R 2 = 8   Ω ,   X C = 3   Ω ,   X L = 5   Ω e V s = 10 ∠ 30 °   V .”

Aplicando a lei das malhas na malha da esquerda:

- 10 ∠ 30 ° + 4 I 1 + V 1 - j 3 I 1 - I 2 = 0

4 - j 3 I 1 + j 3 I 2 + V 1 = 10 ∠ 30 ° … ( 1 )

Aplicando a lei das malhas na malha da direita

- j 3 I 2 - I 1 - V 2 + 8 + j 5 I 2 = 0

j 3 I 1 + 8 + j 2 I 2 - V 2 = 0 … ( 2 )

Nos terminais do transformador, temos:

V 1 V 2 = 4   →     V 1 - 4 V 2 = 0 … 3

I 1 I 2 = 1 4   →     4 I 1 - I 2 = 0 … ( 4 )

Passo 2

Aqui, caímos num sistema de equações, com quatro equações e quatro incógnitas:

4 - j 3 I 1 + j 3 I 2 + V 1 = 8,66 + j 5 j 3 I 1 + 8 + j 2 I 2 - V 2 = 0 V 1 - 4 V 2 = 0 4 I 1 - I 2 = 0

Escrevendo de modo matricial:

4 - j 3 j 3 1 0 j 3 8 + j 2 0 - 1 0 0 1 - 4 4 - 1 0 0 ⋅ I 1 I 2 V 1 V 2 = 8,66 + j 5 0 0 0   → A X = [ b ]

Uma maneira de encontrarmos os valores para as incógnitas é usar a regra de Cramer! Primeiro de tudo, precisamos achar o determinante da matriz:

det ⁡ A = 4 - j 3 j 3 1 0 j 3 8 + j 2 0 - 1 0 0 1 - 4 4 - 1 0 0

det ⁡ A = - 132 - j 53

Agora, vamos calcular os determinantes substituindo o vetor [ b ] nas colunas de cada variável. Assim, para I 1 :

d e t ⁡ ( A I 1 ) = 8,66 + j 5 j 3 1 0 0 8 + j 2 0 - 1 0 0 1 - 4 0 - 1 0 0

det ⁡ A I 1 = - 8,66 - j 5

Para I 2 :

det ⁡ A I 2 = 4 - j 3 8,66 + j 5 1 0 j 3 0 0 - 1 0 0 1 - 4 4 0 0 0

det ⁡ A I 2 = - 34,64 - j 20

Passo 3

Para encontrarmos os valores de cada uma das variáveis, precisamos dividir o determinante de cada uma pelo determinante da matriz A . Logo,

I 1 = det ⁡ A I 1 det ⁡ A = - 8,66 - j 5 - 132 - j 53 = 0,07 + j 0 , 01   A

I 2 = det ⁡ A I 2 det ⁡ A = - 34,64 - j 20 - 132 - j 53 = 0,28 + j 0,04   A

O valor de I X pode ser calculado como:

I x = I 1 - I 2

I X = 0,07 + j 0,01 - ( 0,28 + j 0,04 )

I X = - 0,21 - j 0,03

I X = 210,92 ∠ - 171,88 °   m A

Resposta

A corrente é igual a:

I X = 210,92 ∠ - 171,88 °   m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a impedância de entrada do circuito com transformador de núcleo de ar da Figura 13.102 .
Dois transformadores lineares são colocados em cascata, conforme mostrado na Figura 13.101 . Demonstre que Z e n t = ω 2 R L a 2 + L a L b - M a 2 + j ω 3 L a 2 L b + L a L b 2 - L a M b 2 - L b M a 2
No circuito da Figura 13.9 8 , determine o valor do coeficiente de acoplamento k que fará que o resistor de 10Ω dissipe 320W . Para esse valor de k , determine a energia armazenada nas bobinas acoplad
Determine a impedância de entrada do circuito da figura 13.99 usando o conceito de impedância refletidaObtenha a impedância de entrada substituindo o transformador linear por seu circuito equivalente
Considere a Figura 13.100 e elabora um problema para ajudar outros estudantes a entender melhor os transformadores lineares e como determinar os circuitos equivalente T e equivalente ∏