Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 32

Dois transformadores lineares são colocados em cascata, conforme mostrado na Figura 13.101 . Demonstre que

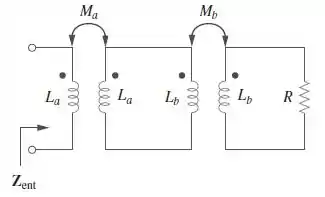
Z e n t = ω 2 R L a 2 + L a L b - M a 2 + j ω 3 L a 2 L b + L a L b 2 - L a M b 2 - L b M a 2 ω 2 L a L b + L b 2 - M b 2 - j ω R L a + L b

Passo 1

Pessoal, a impedância de entre do segundo transformador pode ser obtida usando a ideia de impedância refletida:

Z b = j ω L b + ω 2 M 2 R + j ω L b

Z b = j ω R L b - ω 2 L b 2 + ω 2 M b 2 R + j ω L b

Passo 2

Uma coisa que podemos fazer é considerar o segundo transformador como uma carga para o primeiro. Partindo disso, podemos também refletir a impedância par acharmos Z e n t :

Z e n t = j ω L b + ω 2 M a 2 j ω L a + Z b

Aqui as contas vão ficar mais confusas, logo, vamos por partes! Vamos analisar o denominador da fração primeiro:

j ω L a + Z b = j ω L a + j ω R L b - ω 2 L b 2 + ω 2 M b 2 R + j ω L b

j ω L a + Z b = j ω L a R - ω 2 L a L b + ω 2 M b 2 - ω 2 L b 2 + j ω L b R R + j ω L b

Voltando para a fração:

ω 2 M a 2 j ω L a + Z b = ω 2 M a 2 j ω L a R - ω 2 L a L b + ω 2 M b 2 - ω 2 L b 2 + j ω L b R R + j ω L b

ω 2 M a 2 j ω L a + Z b = R + j ω L b ω 2 M a 2 j ω L a R - ω 2 L a L b + ω 2 M b 2 - ω 2 L b 2 + j ω L b R

Assim, a impedância total é dada por:

Z e n t = j ω L a + ω 2 M a 2 j ω L a + Z b

Z e n t = j ω L a + R + j ω L b ω 2 M a 2 j ω L a R - ω 2 L a L b + ω 2 M b 2 - ω 2 L b 2 + j ω L b R

Z e n t = j ω L a j ω L a R - ω 2 L a L b + ω 2 M b 2 - ω 2 L b 2 + j ω L b R + ω 2 M a 2 R + j ω L b j ω L a R - ω 2 L a L b + ω 2 M b 2 - ω 2 L b 2 + j ω L b R

Z e n t = ω 2 R L a 2 + L a L b - M a 2 + j ω 3 L a 2 L b + L a L b 2 - L a M b 2 - L b M a 2 ω 2 L a L b + L b 2 - M b 2 - j ω R ( L a + L b )

Pronto! Tá aí a demonstração 😊

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um transformador com 2400e s p i r a s no primário e 48e s p i r a s no secundário é usado como casador de impedâncias. Qual é o valor refletido de uma carga de 3Ω conectada ao secundário?
Um transformador de potência abaixador de tensão com relação de espiras n = 0,1 fornece 12,6V r m s para uma carga resistiva. Se a corrente no primário for 2,5A r m s , qual é a potência liberada para
Uma linha de transmissão de 4.800V r m s alimenta um transformador de distribuição com 1.200e s p i r a s no primário e 28e s p i r a s no secundário. Quando uma carga de 10Ω é ligada no secundário, d
Um transformador com quatro enrolamentos (Figura 13.146) é usado normalmente em equipamentos (por exemplo, PCs, VCRs) que podem operar tanto em 110V como em 220V . Isso torna esse equipamento adequado
Um transformador com quatro enrolamentos (Figura 13.146) é usado normalmente em equipamentos (por exemplo, PCs, VCRs) que podem operar tanto em 110V como em 220V . Isso torna esse equipamento adequado