Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 41

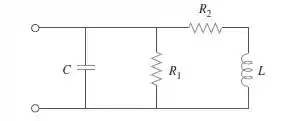
Considere a Figura 14.80 e elabora um probema para ajudar outros estudantes a entender melhor o fator de qualiade, a frequência de ressonância e a largura de banda de circuitos RLC.

Passo 1

Pessoal, vamos resolver a seguinte questão:

“Para o circuito dado, encontre a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B . Considere C = 0,1   F , R 1 = 10   Ω , R 2 = 2   Ω e L = 2   H ”.

Gente, a frequência de ressonância ω 0 para um circuito R L C é a frequência em que a impedância (admitância) do circuito se torna puramente resistiva (condutiva). Assim, para a gente encontrar ω 0 , precisamos encontrar a admitância do circuito e igualar a parte imaginária a zero.

Y e n t = j ω C + 1 R 1 + 1 R 2 + j ω L

Y e n t = j ω 0,1 + 1 10 + 1 2 + j ω ( 2 )

Y e n t = j ω 0,1 + 0,1 + 1 2 + j 2 ω

Vamos multiplicar a fração, o numerador e o denominador, pelo conjugado, temos:

Y e n t = j ω 0,1 + 0,1 + 2 - j ω 2 4 + 4 ω 2

Y e n t = 0,1 + 2 4 + 4 ω 2 + j 0,1 ω - 2 ω 4 + 4 ω 2

Passo 2

Vamos agora igualar a zero a parte imaginária da admitância:

0,1 ω - 2 ω 4 + 4 ω 2 = 0

0,1 ω = 2 ω 4 + 4 ω 2

4 + 4 ω 2 = 2 ω 0,1 ω

Simplificando a equação:

4 + 4 ω 2 = 20

ω 2 = 16 4 = 4

ω = 4 = 2   r a d / s

Passo 3

Para obtermos a largura de banca do circuito, nós precisamos achar as frequências de meia potência. Elas podem ser obtidas igualando o módulo de Y e n t a 2 R e ( Y e n t ) :

2 R e Y e n t = 2 0,1 + 2 4 + 4 ω 2

2 R e Y e n t = 2 0,1 + 2 4 + 4 2 2

2 R e Y e n t = 0,2828   S

Igualando ao módulo da admitância:

0,1 + 2 4 + 4 ω 2 2 + 0,1 - 2 ω 4 + 4 ω 2 2 = 0,2828

Resolvendo essa equação, temos:

ω 1 = 1,414   r a d / s

ω 2 = 3,741   r a d / s

A largura de banda B é dada pela diferença entre ω 1 e ω 2 . Logo,

B = ω 2 - ω 1

B = 3,741 - 1,414

B = 2,327   r a d / s

Passo 4

Por fim, o fator de qualidade é dado por:

Q = ω 0 B

Q = 2 2,327

Q = 0,859

Resposta

ω 0 = 2   r a d / s

B = 2,327   r a d / s

Q = 0,859

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Determine a corrente no resistor de 160 V no circuito da Figura P13.36. O sentido de referência para a corrente é de cima para baixo, passando pelo resistor.b) Repita a parte (a), se o ponto no enr
A chave no circuito da Figura P13.40 esteve fechada por um longo tempo, antes de abrir em t = 0. Use o método da transformada de Laplace para determinar vo.
Não há nenhuma energia armazenada no circuito apresentado na Figura P13.43 no instante em que as duas fontes são conectadas. a) Use o princípio da superposição para determinar Vo. b) Determine v o , p