Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 43

Não há nenhuma energia armazenada no circuito apresentado na Figura P13.43 no instante em que as duas fontes são conectadas.

a) Use o princípio da superposição para determinar Vo.

b) Determine v o , para t>0.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Observando o sistema acima, podemos concluir que a fonte de voltagem agindo sozinha, se comporta da seguinte forma:

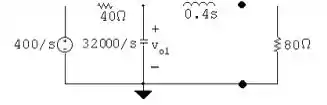
    2. Disso, podemos concluir que:

    V 01 = 32 x 10 4 ( s + 200 ) s ( s + 400 ) ( s + 600 )

    Já na segunda situação, temos:

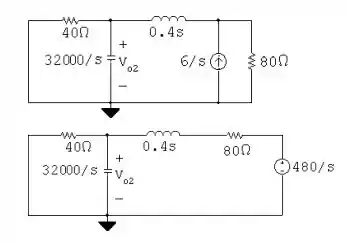
    E disso, podemos tirar que:

    V 02 = 38,4 x 10 6 s ( s + 400 ) ( s + 600 )

    Portanto:

    V 0 = V 01 + V 02 = 32 x 10 4 s + 320 s ( s + 400 ) ( s + 600 )

    Passo 2

  2. Decompondo V 0 em termos de K, temos que:

K 1 = 32 x 10 4 320 ( 400 ) ( 600 ) = 426,67

K 2 = 320

K 3 = - 746,67

Portanto:

v 0 t = 426,67 + 320 e - 400 t - 746,67 e - 600 t u t V

Resposta

  1. Item a:

    2. V 0 = 32 x 10 4 s + 320 s ( s + 400 ) ( s + 600 )

  2. Item b:

v 0 t = 426,67 + 320 e - 400 t - 746,67 e - 600 t u t V

Exercícios de Livros Relacionados

Considere o circuito da figura e determine i ( t ) para t0 .
Considere o circuito da figura e determine i ( t ) e v ( t ) para t0 .
Determine i ( t ) para t0 no circuito da figura:
Determine a tensão de saída v o ( t ) no circuito da figura.
Determine v para t0 no circuito da figura: