Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.6 - Ex. 3
Deduza uma equação para a divisão da tensão entre os dois indutores em série, por meio de V1 e V2.
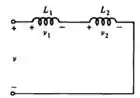
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para achar a equação para a divisão de tensão. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
Passo 2
Ok, agora o nosso problema vai ser relembrar qual a fórmula de um indutor em série. Responde Aí!! Lembrou?? Não?!
Vamos usar a associação em série como:
Bora lembrar da relação da tensão e corrente em um indutor.
Essa relação é
Passo 3
Então vamos lá!
Caracterizando temos:
Lembrando que e são percorridas pelo mesmo valor de corrente.
Substituindo (3) em (1):
Temos que:
Como
Então:
Substituindo (3) em (2):
Temos que:
Como
Então:
Tranquilo essa hein!!