Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 39
Determine para no circuito da Figura .
Passo 1
Vamos lá, galerinha! Quando estamos em , ou seja, no momento antes de , nós tmeos que as fontes de tensão são iguais a zero e as condições iniciais são e . Quando , passamos a ter o seguinte circuito:
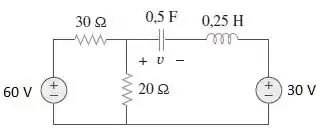
Logo, temos:
Vamos agora encontrar as raízes características:
Como os valores de e são diferentes e , temos a resposta natural com amortecimento supercrítico. As raízes são:
Desse modo, podemos escrever a tensão da seguinte forma:
Passo 2
Quando olhamos para o instante , temos:
A corrente de um indutor pode ser escrita como:
No instante ,
Porém,
O que nos leva ao seguinte sistema de equações:
Resolvendo esse sistema, temos:
Logo,
Resposta
A tensão é igual a:
Exercícios de Livros Relacionados
Calcule v para t0 , se v (0) = 4 V e i (0) = 3 A .
Calcule v para t0 .
a) Calcule v para t0 .b) Substitua as fontes de corrente e de tensão por 2 cos 2 t e6 cos 2 tV , respectivamente, com as mesmas polaridades e calcule v para t0 se não existir nenhuma energia inici
Usando os resultados do Problema 9.39 calcule i ,t0 , se nao existe energia inicial armazenada.
a) Suponhamos que o circuito da Figura 8.21 tenha um indutor de 5 nH e um capacitor de 2 pF. Calcule a frequência, em GHz, da saída senoidal para t $ 0. b) A fonte de tensão cc e um resistor conectado