Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 15
Determine e , no circuito da figura .
Passo 1
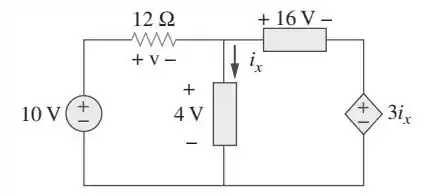
Dá uma olhadinha no circuito:
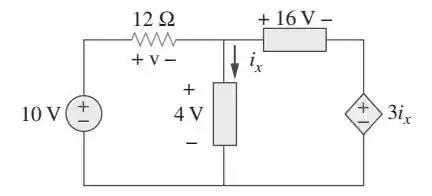
Para resolver essa questão, vamos usar a lei de Kirchoff para tensões. O que a gente vai fazer é o seguinte: vamos caminhar pelo circuito somando e subtraindo tensões e voltar para o mesmo ponto. Qual é a diferença de tensão entre um ponto e ele mesmo? Só pode ser zero! Lembra do seguinte: se passar do menos pro mais, soma a tensão, e se passar do mais pro menos, subtrai.
Passo 2
No ramo da esquerda, no sentido horário:
E pro ramo da direita, agora no sentido anti-horário:
Resposta
Exercícios de Livros Relacionados
No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e 0 resistor de 12Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v
No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e o resistor de 12 Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v.
Considere o circuito mostrado na Figura P2.17. a) Determine v 0 usando as leis de Kirchhoff e a lei de Ohm. b) Teste a solução para v 0 , verificando que a potência total fornecida é igual à potência
a) Determine as correntes i 1 e i 2 no circuito da Figura P2.19. b) Determine a tensão v 0 . c) Verifique que a potência total fornecida é igual à potência total consumida.
A corrente i x no circuito mostrado na Figura P2.20 é 50 mA e a tensão v x é 3,5 V. Determine (a) i 1 ; (b) v 1 ; (c) v g ; e (d) a potência fornecida pela fonte de corrente.