Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 49
Se a forma de onda na Figura 7.116a for aplicada ao circuito na Figura 7.116b, determine . Suponha que .
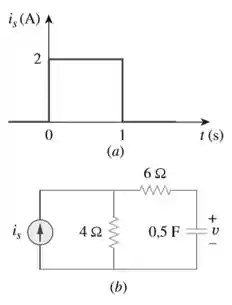
Passo 1
Okay galera, essa questão tem um circuito nem tão básico, mas vamos definir em 2 momentos: Antes do , e . Então, bora lá!
Para ,
Para ,
Passo 2
Portanto,
Resposta
Exercícios de Livros Relacionados
Se a função de transferência de um sistema for H s = s 2 + s + 2 s 3 + 4 s 2 + 5 s + 1 Segue que a entrada será X s = s 3 + 4 s 2 + 5 s + 1 , enquanto a saída será Y s = s 2 + s + 2 .a) verdadeiro b)
Determine v t ,t0 no circuito da figura. Seja v s = 20V .
Determine i ( t ) no circuito da figura por meio de transformadas de Laplace.
O capacitor no circuito da figura se encontra descarregado inicialmente. Determine v 0 ( t ) para t0 .
A resposta ao degrau de um circuito R L C é dada por d 2 i d t ² + 2 d i d t + 5 i = 10 ² Sabendo que i 0 = 6 e d i 0 d t = 12 , calcule i ( t ) .