Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 55

Determine v ( t ) para t < 0 e t > 0 no circuito da Figura 7.121

Passo 1

Calma galerinha, não priemos cânico! Cheio de coisa mas vamos destrinchar por partes!

Antes de t = 0 , vamos considera o circuito abaixo!

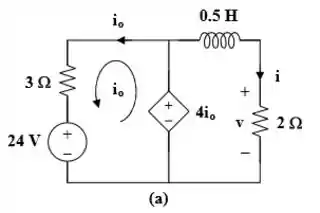
Analisando o circuito:

3 i_0 + 24 - 4 i_0 = 0 -> i_0 = 24 A

v (t) = 4 i_0 = 96 V

i = (v)/(2) = 48 A

Passo 2

Legal? Agora depois de t = 0 , temos o seguinte:

i (t) = i (oo) + [i (0) - i (oo)] e^(- (t)/(tau))

i (0) = 48 A , i (oo) = 0

R_t h = 2 omega , tau = (L)/(R_t h) = (0.5)/(2) = (1)/(4)

i (t) = (48) e^(- 4 t)

Logo,

v (t) = 2 i (t) = 96 e^(- 4 t) u (t) V

Resposta

Antes de t = 0 , i = 48 A e V = 96 V

Depois de t = 0 , i = (48) e^(- 4 t) e v (t) = 96 e^(- 4 t) u (t) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A fonte de 240 V, e resistência interna de 2 V, no circuito da Figura P7.20, sofre inadvertidamente um curto-circuito em seus terminais a,b. No instante em que a falha ocorre, o circuito estava em fun
Segue o mesmo raciocínio da questão anterior, só que agora quer saber coisas relacionadas a energia armazenada.
A questão quer que o aluno mostre que o resistor tem uma certa equação, e em seguida comparar com o resultado da questão anterior.
Essa questão é interessante, uma vez que se pode escolher qual configuração pode ser usada
A questão quer a porcentagem de energia inicial armazenada que será dissipada pelo resistor de 60Ω . Simbora!