Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 55

55- Determine Z no circuito da Figura 9.62 dado que V_o = 4 /_ 0 ° V

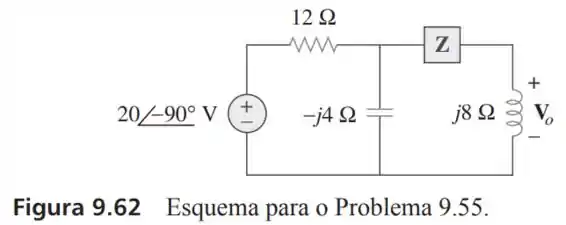
Passo 1

Como temos o valor de V_o então teremos como calcular a corrente que passa por V_o e Z , nós teremos:

V_o = j 8 xx I_2

Dessa forma:

I_2 = (4 /_ 0)/(j 8) = 0.5 /_ - 90 ° A

Então teremos o seguinte circuito.

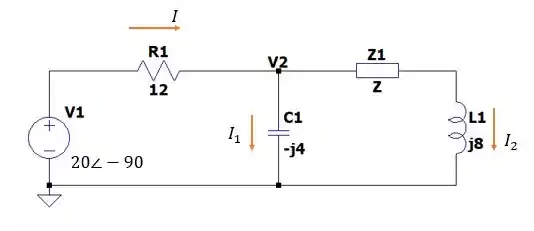
E nós teremos que calcular V_2 para que possamos ser capazes de dizer quanto vale Z .

Passo 2

A somatória das correntes no nó V_2 valerá:

I = I_1 + I_2

Que é a mesma coisa que .

(20 /_ - 90 - V_2)/(12) = (V_2)/(- j 4) + 0.5 /_ - 90

(5)/(3) /_ - 90 - 0.5 /_ - 90 = (V_2)/(12) + (V_2)/(- j 4)

(- 7 j)/(6) = V_2 ((12 - j 4)/(- j 48))

V_2 = (8 xx 7 j^2)/(12 - j 4) = (- 14)/(3 - j) = (- 14 /_ 0)/(3.1623 /_ - 18.435) = - 4.427 /_ 18.435 ° V

Passo 3

Então:

V_2 = Z I_2 + j 8 ( I_2 )

- 4.427 /_ 18.435 = Z (0.5 /_ - 90) + (0.5 /_ - 90) 8 /_ 90

Z (0.5 /_ - 90) = 4.427 /_ - 71.565 - 4

Z = (- 4.427 /_ 18.435 - 4)/(0.5 /_ - 90) = (- 8.2 - j 1.4)/(0.5 /_ - 90) = (8.319 /_ 189.689)/(0.5 /_ - 90) = 16.638 /_ 279.69 ° omega

De modo complexo teremos:

Z = (16.638 cos 279.69 + j 16.638 sin 279.69) = (2.8 - j 16.4) omega

Resposta

Z = 16.638 /_ 279.69 ° omega = (2.8 - j 16.4) omega

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escolha C = 0.1 μ F e calcule R e L no Prob. 15.6, de forma que ω 0 = 10 4 rad/s e B = 10 4 rad/s.
10.22. Calcule a reatância X tal que a impedância vista pela fonte seja real. Para este caso, calcule a corrente em regime permanente i(t) correspondente a I se w = 10 rad/s.
10.25. Calcule a corrente i em regime permanente.
10.26. Calcule a tensão v em regime permanente.
10.34. Calcule a tensão v em regime permanente.