Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 55
55. Determine os circuitos equivalentes de e nos terminais para cada um dos circuitos da figura
=
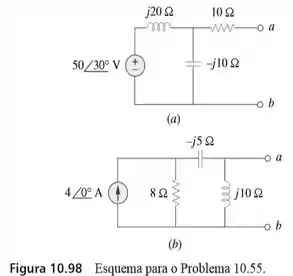Passo 1
a) Bom! A primeira coisa que temos que fazer pra achar os equivalentes de e , que são bem parecidos; é ignorar qualquer fonte de tensão ou de corrente que estiverem presentes no circuito. Nesse caso, como temos uma fonte de tensão, iremos substituir essa fonte por um curto circuito.
Desse jeito aqui...
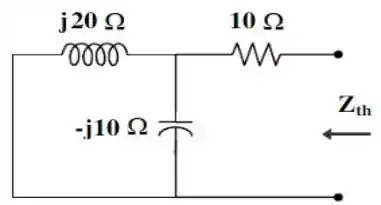
E então, bora calcular a impedância equivalente, para a parte do circuito. Ela é dada por:
A impedância de é igual a de .... Sendo assim:
Passo 2
Em seguida, bora descobrir a tensão de para o circuito com base na figura abaixo:
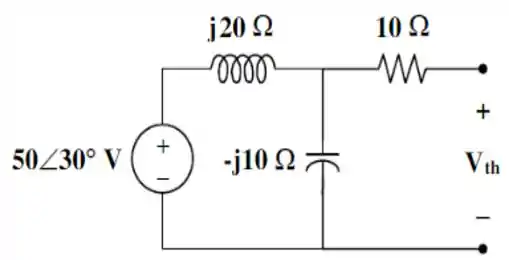
Olhando essa figura, por divisão de tensão, temos que:
E a corrente de , pode ser obtida simplesmente dividindo essa tensão de pela impedância que já descobrimos no :
Passo 3
b) Para se resolver essa letra b, vamos tomar os mesmos procedimentos realizados na letra a... Primeiro, redesenhar o circuito ignorando fontes de tensão ou de corrente:
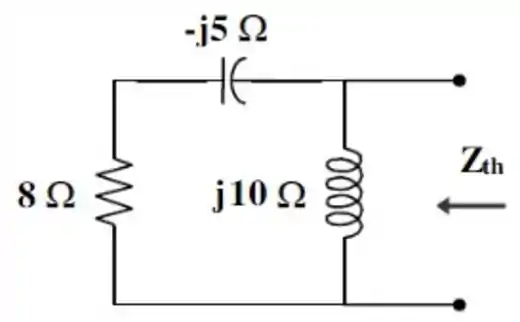
No caso, como temos uma fonte de corrente, iremos substituir essa fonte por um circuito aberto.
A impedância equivalente, , para essa parte do circuito é dada por:
Passo 4
Depois, bora tratar de obter com base na figura abaixo:
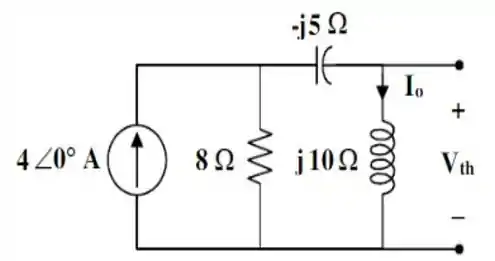
Por divisão de corrente, temos que o valor da na figura acima, é dado por:
E a tensão é dada pelo produto dessa corrente pela impedância do indutor, de .
A corrente de , pode ser obtida simplesmente dividindo essa tensão de pela impedância que já descobrimos no :
Resposta
a)
b)