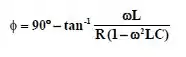Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 20
Consulte a Figura 10.69. Se e , deduz as expressões para A e
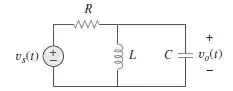
Passo 1
Vamos lá! Primeiro não vamos assustar porque não tem número e sim letras, pois é a mesma coisa!
O primeiro passo é levarmos o circuito para o domínio da frequência, desse modo
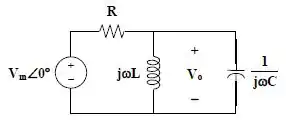
Passo 2
Vamos encontrar o equivalente entre o indutor e o capacitor em paralelo, desse modo
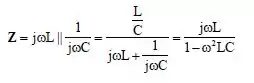
Então para acharmos , basta fazermos um divisor de tensão, portanto
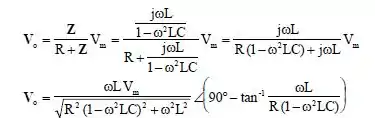
Passo 3
A questão nos diz que,
Então por comparação temos
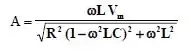
E que,
Resposta
Exercícios de Livros Relacionados
Calcule a tensão v em regime permanente.
Calcule a tensão v em regime permanente.
Calcule a tensão v em regime permanente.
Note que o circuito fasorial correspondente é uma ponte equilibrada e use o método do Prob. 11.18, com Z 5 substituído por um circuito aberto, para encontrar a resposta forçada v .
Calcule a resposta forçada i se v g = 4 cos 1000 t V.