Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 16
Use a análise nodal para determinar no circuito mostrado na Figura 10.65.
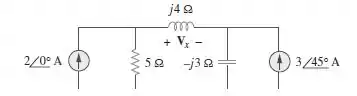
Passo 1
Vamos lá! A questão propõe que resolvemos esse circuito por análise nodal, o que pode dificultar essa questão são as fontes de corrente. Mas vamos lembrar dos assuntos anteriores em corrente contínua! É a mesma coisa em corrente alternada.
Vamos dividir os nós da seguinte maneira.
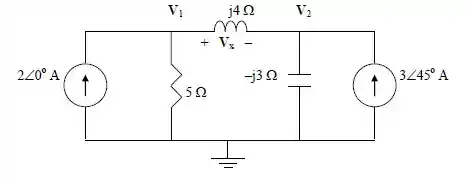
O circuito já está no domínio da frequência, então vamos para os cálculos!
Passo 2
Note que, para o nó 1, temos:
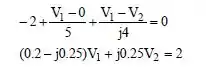
Observe como a fonte de corrente foi tratada para esse nó, se ainda tiver dúvidas dessa equação ela é basicamente a soma de cada corrente que sai do nó 1.
Do mesmo modo para o nó 2,
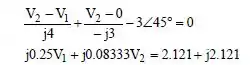
Passo 3
Temos duas equações com duas variáveis, podemos resolver por meio de matrizes, logo
Para essa resolução vamos utilizar o MATLAB, então o código para resolver esse sistema é:
>> Y=[(0.2-0.25i),0.25i;0.25i,0.08333i]
Y =
0.2000 - 0.2500i 0 + 0.2500i
0 + 0.2500i 0 + 0.0833i
>> I=[2;(2.121+2.121i)]
I =
2.0000
2.1210 + 2.1210i
>> V=inv(Y)*I
V =
5.2793 - 5.4190i
9.6145 - 9.1955i
Com isso, temos