Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 16

Determine a constante de tempo para cada um dos circuitos da figura 7.96.

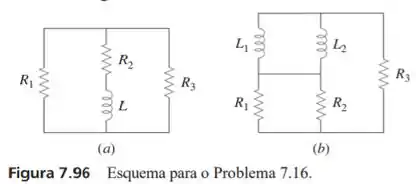
Passo 1

Para um circuito R L a constante de tempo τ é dada por

τ = L e q R e q

Para o caso do primeiro circuito temos que L e q = L e

R e q = R 2 + R 1 ⋅ R 3 R 1 + R 3 = R 2 ⋅ R 1 + R 3 + R 1 ⋅ R 3 R 1 + R 3

Portanto, nossa constante de tempo será dada por

τ = L ⋅ R 1 + R 3 R 2 ⋅ R 1 + R 3 + R 1 ⋅ R 3

Passo 2

Já para o segundo caso temos dois indutores em paralelo e, assim,

L e q = L 1 ⋅ L 2 L 1 + L 2

E a resistência equivalente vai ser dada por

R e q = R 3 + R 1 ⋅ R 2 R 1 + R 2 = R 3 ⋅ R 1 + R 2 + R 1 ⋅ R 2 R 1 + R 2

Portanto, nossa segunda constante de tempo será dada por

τ = L 1 ⋅ L 2 ⋅ R 1 + R 2 L 1 + L 2 R 3 ⋅ R 1 + R 2 + R 1 ⋅ R 2

Resposta

a   τ = L ⋅ R 1 + R 3 R 2 ⋅ R 1 + R 3 + R 1 ⋅ R 3

b   τ = L 1 ⋅ L 2 ⋅ R 1 + R 2 L 1 + L 2 R 3 ⋅ R 1 + R 2 + R 1 ⋅ R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura 7.99 , determine i t para t0 se i 0 = 6 A .
No circuito da figura 7.10, determine o valor de R para o qual a energia em regime estacionário armazenada no indutor seja 1 J .
No circuito da figura 7.93, v t = 80 ⋅ e - 10 3 tV , t0 i t = 5 ⋅ e - 10 3 tm A , t0 a Determine R , Leτ . b Calcule a energia dissipada na resistência para 0t0.5 m s .
Determine a constante de tempo para cada um dos circuitos da figura 7.95.