No circuito da Figura , determine para se .
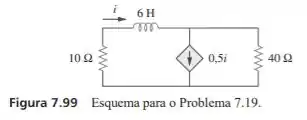
Passo 1
Para que consigamos encontrar como o exercício pede vamos precisar calcular a resistência de Thevenin, então, vamos utilizar um truque que facilitará nossa vida que é trocar o indutor por uma fonte de tensão de , dessa forma poderemos aplicar a lei das malhas obtendo as seguintes equações
Mas a partir do nó central podemos inferir que
Assim, substituindo na primeira equação vamos obter
Então, nossa resistência de Thevenin será dada por
Passo 2
Dessa forma, nossa constante de tempo para esse caso será dada por
Agora, temos tudo o que precisamos para concluir o exercício, basta fazermos