Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 15
Determine a constante de tempo para cada um dos circuitos da figura 7.95.
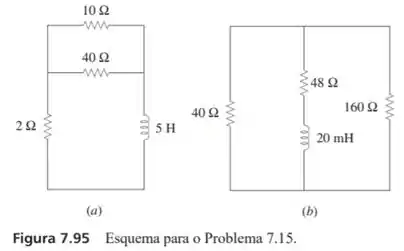
Passo 1
Para um circuito a constante de tempo é dada por
Precisamos então calcular a resistência equivalente que vai ser dada por
Para o circuito . Agora, para o circuito teremos
Passo 2
Sendo assim, nossas constantes de tempo para os circuitos e serão, respectivamente,
Resposta
Exercícios de Livros Relacionados
A chave no circuito da Figura P7.8 esteve fechada por um longo tempo, antes de ser aberta em t = 0 .a) Determine i 1 0 - e i 2 0 - .b) Determine i 1 0 + e i 2 0 + .c) Determine i 1 t para t ≥ 0 .d) De
[a] - Deduza as expressões para as correntes i1(t) e i2(t) para t ≥ 0 . [b] - Use as expressões deduzidas em (a) para determinar i1( ∞ ) e i2( ∞ ).
Relacionada a questão 47. a) a energia total dissipada no resistor de 40 V;b) a energia retida nos indutores; c) a energia inicial armazenada nos indutoresQuestão bem direta, vamos resolver!!
[a] - Determine v 0 t em função de I g , R1, R2 e L.[b] - Explique o que acontece com v 0 ( t ) quando R2 aumenta indefinidamente.[c] - Determine v S W em função de I g , R1, R2 e L.[d] - Explique o q
A chave no circuito da Figura P7.44 esteve aberta por um longo tempo, antes de ser fechada em t = 0. Determine i 0 ( t ) para t ≥ 0 .