Determine io e a potência dissipada no resistor de 140 V do circuito da Figura P3.62.
Passo 1
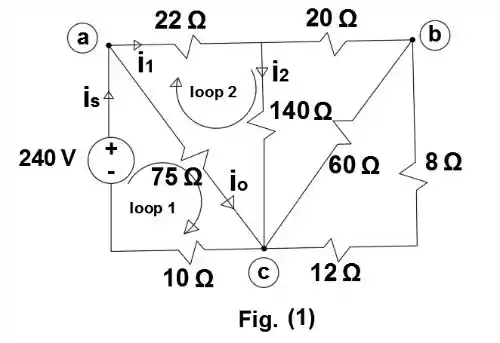
No ramo bc: 8 + 12, a resistência equivalente é então = 20. Utilizando transformação delta/estrela (22,20,140)
resistência equivalente:
a resistência equivalente:
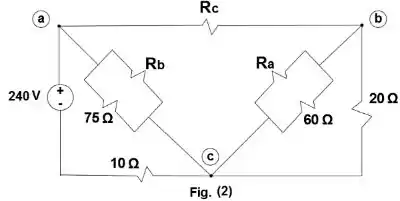
Passo 2
, a resistência equivalente é então:
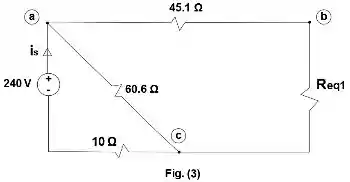
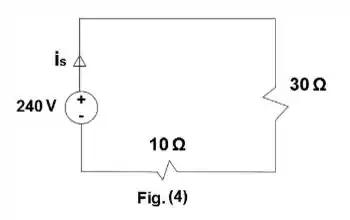
Passo 3
Utilizando a Lei de Ohm:
Da figura 1:
Da figura (1), no nó a:
Lei de Kirchhof no Loop 2: