Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 39
Determine a potência real absorvida pela carga na Figura 12.58.
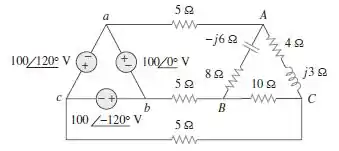
Passo 1
Primeiro não vamos nos assustar com o tamanho do circuito, note que vamos ter que usar análise de malhas, visto que é um circuito desequilibrado, assim não podemos fazer a transformação .
Logo, o circuito ficará:
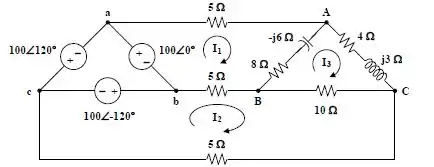
Passo 2
Agora que já temos as malhas, vamos escrever a equação para cada uma, do mesmo modo que fazia em circuitos monofásicos. Portanto,
Para malha 1:
Para malha 2:
Para malha 3:
Passo 3
Certo! Agora vamos manipular essas equações para eliminar alguma incógnita.
Para eliminar , primeiro multiplica a equação da malha 1 por 2:
Subtraindo a malha (3) de (4)
Multiplica a malha 2 por 5/4:
Somando a malha 1 e (6)
Passo 4
Para resolver essas equações podemos utilizar o método matricial, então as equações de 5 e 7 torna-se
Assim,
E como,
Como também,
Certo agora que já sabemos e , podemos usar a equação (6) para descobrir :
Passo 5
Agora que já sabemos a corrente que passa em cada carga, então podemos utilizar a equação abaixo para calcular a potência real,
Logo, para o resistor de 8:
Para o resistor de 4:
Para o resistor de 10:
Assim, para a potência real absorvida é: