Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 39
Para o circuito exibido na Figura , determine e use esta para determinar a corrente . Considere .
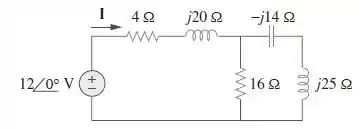
Passo 1
Pessoal, a primeira coisa que devemos fazer é encontrar a impedância equivalente do circuito. De início vamos calcular o equivalente paralelo :
Uma vez que achamos, vamos achar o
Passo 2
A corrente pode ser encontrada se dividirmos a tensão da fonte pela impedância total do sistema, . Desse modo,
Vamos passar o denominar para a forma polar:
Portanto,
Convertendo para o domínio do tempo:
Resposta
A corrente é igual a:
Exercícios de Livros Relacionados
A Figura 9.91 mostra uma associação em paralelo entre uma indutância e uma resistência. Se for desejado conectar um capacitor em série com a associação em paralelo de modo que a impedância resultante
Um sistema de transmissão de energia apresenta o modelo indicado na Figura 9.92. Dado o seguinte:Determine a corrente I L na carga.
Determine I 0 no circuito apresentado na figura 9.50 .
Para o circuito da Figura 9.70 , determine o valor de Z T
53- Determine I o no circuito da Figura 9.60