Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 61

Determine a tensão v o ( t ) no circuito da figura por meio da transformada de Laplace

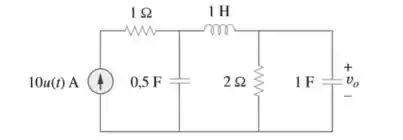
Passo 1

Falai moçadinha, show de bola?

Bora lá?

O indutor de impedância no domínio s é.

Z s = s L

Para L = 1 H ,   Z s = s

O capacitor de impedância no domínio s é

Z s = 1 s C

Por,

C = 0.5 F ,     Z s = 2 s

C = 1   F ,     Z s = 1 s

O equivalente no domínio s do circuito é mostrado na Figura a seguir

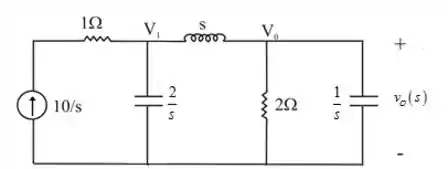
Passo 2

Vamos fazer a análise Nodal no nó V 1

10 s = s V 1 2 + V 1 - V O s

V 1 s 2 + 1 s - V o s = 10 s

V 1 s 2 + 2 2 s - V o s = 10 s

V 1 0.5 s 2 + 1 - V o = 10         ( 1 )

Vamos fazer a análise Nodal no nó V o

V o - V 1 s + V o 2 + s V o = 0

V o 1 s + 1 2 + s - V 1 s = 0

V o 2 s 2 + s + 2 2 s - V 1 s = 0

V o s 2 + 0.5 s + 1 - V 1 = 0

V 1 = V o s 2 + 0.5 s + 1         ( 2 )

Passo 3

Agora iremos substituir a expressão (2) na expressão (1)

V o s 2 + 0.5 s + a 0.5 s 2 + 1 - V o = 10

V o 0.5 s 4 + s 2 + 0.25 s 3 + 0.5 s + 0.5 s 2 + 1 - 1 = 10

V o 0.5 s 4 + 0.25 s 3 + 1.5 s 2 + 0.5 s = 10

V o 0.5 s s 3 + 0.5 s 2 + 3 s + 1 = 10

V o = 20 s s 3 + 0.5 s 2 + 3 s + 1

Passo 4

Vamos resolver a raiz da equação característica s s 3 + 0.5 s 2 + 3 s + 1 = 0

  s s 3 + 0.5 s 2 + 3 s + 1 = 0

s s + 0.3395 s 2 + 0.1605 s + 2.945 = 0

V o = 20 s s + 0.3395 s 2 0.1605 s . 2.945

Depois que a fração parcial é V o

V o = 20 s - 19.595 ( s + 0.3395 ) + - 0.404 s - 6.71763 ( s 2 + 0.1605 s + 2.945 )

= 20 s - 19.595 s + 0.3395 + - 0.404 s - 6.71763 s + 0.08025 2 - 0.080205 2 + 2.945

V o = 20 s - 19.595 s + 0.3395 + - 0.404 s - 6.71763 s + 0.08025 2 + 1.714 2

Passo 5

Vamos simplificar ainda mais

V o = 20 s - 19.595 s + 0.3395 + - 0.404 s - 6.71763 s + 0.08025 2 + 1.714 2

= 20 s - 19.595 s + 0.3395 - 0.404 s + 0.08025 - 0.08025 s + 0.08025 2 + 1.714 2 - 6.71763 s + 0.08025 2 + 1.714 2

= 20 s - 19.595 s + 0.3395 - 0.404 s + 0.08025 s + 0.08025 2 + 1.714 2 - 6.685 s + 0.08025 2 + 1.714 2

= 20 s - 19.595 s + 0.3395 - 0.404 s + 0.08025 s + 0.08025 2 + 1.714 2 - 3.9 1.714 s + 0.08025 2 + 1.714 2

Passo 6

Agora iremos aplicar a transformada de Laplace inversa para podermos obter v o ( t )

v o t = 20 u t - 19.595 e - 0.3395 t u t - 0.404 e - 0.08025 t cos ⁡ 1.714 u t

- 3.9 - 0.08025 t sin ⁡ 1.714 t u ( t )

= [ 20 - 19.595 e - 0.3395 t - e - 0.08025 t 0.404 cos ⁡ 1.714 t + 3.9 sin ⁡ ( 1.714 t ) ) u ( t )

Portanto, o valor de v o ( t ) é

[ 20 - 19.595 e - 0.3395 t - e - 0.08025 t 0.404 cos ⁡ 1.714 t + 3.9 sin ⁡ ( 1.714 t ) ) u ( t )

Resposta

Portanto, o valor de v o ( t ) é :

[ 20 - 19.595 e - 0.3395 t - e - 0.08025 t 0.404 cos ⁡ 1.714 t + 3.9 sin ⁡ ( 1.714 t ) ) u ( t )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito tem R 1 = 3 ,R 2 = 10 ,L = 2 HeC = 1 10 F . Após ser aplicado um fator de escala a amplitude igual a 100 e a frequência de 1 0 6 , determine os novos valores dos elementos de circuitos.
Em um circuito R L C ,R = 20 ,L = 40 H ,C = 1 F .O circuito sofre uma aplicação de escala na amplitude de 10 e na frequência de 1 0 5 . Calcule os novos valores dos elementos.
Calcule os valores de R, L e C que resultarão em, respectivamente, R = 12 k, L = 40 mH e C = 300 nF quando houver a aplicação de fator de escala de amplitude 800 e fator de escala de frequência 1.000.
O circuito mostrado na figura tem impedância Z ( s ) = 1000 ( s + 1 ) ( s + 1 + j 50 ) ( s + 1 - j 50 ) ,s = j ω Determine: Os valores de R ,L ,CeG Os valores dos elementos que farão que a frequência
Um circuito R L C em série possui R = 10 Ω ,ω o = 40r a d / seB = 5r a d / s . Determine LeC quando o circuito sofre uma aplicação de escala: Na amplitude por um fator 600 . Na frequência por um fator