Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 81
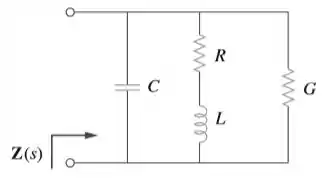
O circuito mostrado na figura tem impedância
Determine:
- Os valores de
- Os valores dos elementos que farão que a frequência de ressonância seja elevada por um fator igual a pela aplicação de fator de escala de frequência
Passo 1
Vamos comparar essa impedância com a expressão que vamos encontrar analisando o sistema e sem valores:
Comparando a nossa expressão do enunciado com essa acima, encontramos nossos valores da letra a)
Capacitor:
Resistor e indutor:
G:
Passo 2
Na letra b, nós queremos encontrar os valores de . Sabendo que Então, vamos utilizar a seguinte fórmula:
Para o resistor:
Para G:
Para o indutor:
Para o capacitor:
Resposta
Exercícios de Livros Relacionados
A corrente em um circuito RLC é descrita por d 2 i d t ² + 10 d i d t + 25 i = 0 ² Se i 0 = 2 e d i 0 d t = 0 , determine i ( t ) para t0 .
Considere a figura e elabore um problema para ajudar outros estudantes a entender melhor a análise de circuito usando as transformadas de Laplace.
A equação diferencial que descreve a tensão em um circuito RLC é d 2 v d t ² + 5 d v d t + 4 v = 0 ² Sabendo que v 0 = 0 e d v 0 d t = 5 , obtenha v ( t ) .
As respostas ao degrau de um circuito R L C são V C = 40 - 10 e - 2000 t - 10 e - 4000 tV ,t0 i L t = 3 e - 2000 t + 6 e - 4000 tm A ,t0 a) Determine C b) Determine que tipo de amortecimento o circuit
Projete um circuito R L C que tenha a equação característica s 2 + 100 s + 10 6 = 0