Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 63

Considere o circuito RLC em paralelo da figura. Determine v ( t )   e   i ( t ) dado que v ( 0 ) = 5 e i ( 0 ) = 2   A

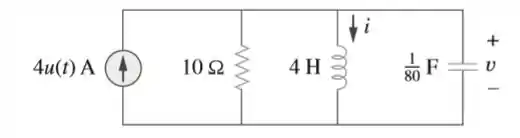
Passo 1

Vamos começar passando esse circuito para o domínio de Laplace (domínio s), incorporando as condições iniciais:

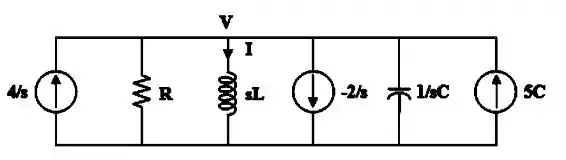
Passo 2

Agora podemos aplicar a lei de Kirchhoff no nó V e isolá-lo:

4 s + 2 s + 5 C = V R + V s L + s C V

V =   5 s + 6 C s 2 + s R C + 1 L C

Passo 3

Mas como 1 R C = 1 10 80 = 8 e 1 L C = 1 4 80 = 20

Então teremos, V = 5 s + 480 4 s ( s 2 + 8 s + 20 ) = 5 ( s + 4 ) ( s + 4 ) 2 + 2 2 + ( 2 x 230 ) ( s + 4 ) 2 + 2 2

E como essa tá bem simples, nem precisa fazer o método das frações parciais!

Por Laplace utilizando a tabela de transformadas, teremos:

v ( t ) = 5 e - 4 t c o s ( 2 t ) + 230 e - 4 t s e n ( 2 t )   V

Passo 4

Agora para a corrente temos:

I = V s L = 5 s + 480 4 s ( s 2 + 8 s + 20 )

Separando em frações parciais teremos:

I = 1.25 s + 120 s ( s 2 + 8 s + 20 ) = A s + B s + C s 2 + 8 s + 20

Agora basta encontrar A ,   B   e   C e encontrar I .

A = 6

B =   - 6

C =   - 46.75

Daí, substituindo, teremos:

I = 6 s - 6 s   + 46.75 s 2 + 8 s + 20 = 6 s - 6 ( s + 4 ) ( s + 4 ) 2 + 2 2 - ( 2 x 11.375 ) ( s + 4 ) 2 + 2 2

Por Laplace utilizando a tabela de transformadas, teremos:

i ( t )   = 6 u ( t ) - 6 e - 4 t c o s ( 2 t ) - 11.375 e - 4 t s e n ( 2 t ) ,   t > 0

Resposta

v ( t ) = 5 e - 4 t c o s ( 2 t ) + 230 e - 4 t s e n ( 2 t )   V

i ( t )   = 6 u ( t ) - 6 e - 4 t c o s ( 2 t ) - 11.375 e - 4 t s e n ( 2 t ) ,   t > 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave na figura é movida da posição A para B em t = 0 (observe que a chave deve ser conectada ao ponto B antes de interromper a conexão com A ) . Determine v t para t0 .
87- Desenvolva as equações de estado para o problema elaborado por você no Problema 16.13 .
Um circuito ressonante em paralelo com fator de qualidade 120 apresenta uma frequência de ressonância 6 × 10 6 r a d s . Calcule a largura de banda e as frequências de meia potência.
Determine a frequência de ressonância do circuito na Figura 14.78
Elabore um problema para ajudar outros estudantes a entender melhor o fator de qualidade, a frequência de ressonância e a largura de banda de um circuito R L C em paralelo.