Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 33
Determine v(t) para t > 0 no circuito da Figura 8.81.
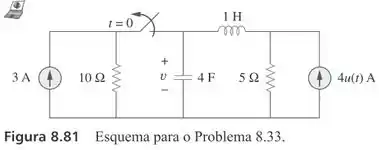
Passo 1
Podemos transformar as fontes de corrente em fontes de tensão. Para t = 0-, o circuito equivalente é mostrado na figura abaixo.
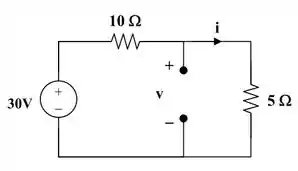
Esse é fácil de resolver, né? Basta aplicar lei de Ohm para encontrar a corrente e divisor de tensão para encontrar v(0).
Passo 2
E quando t > 0, teremos o circuito RLC da figura a seguir:
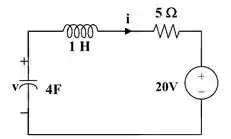
Calma que esse é molezinha também. Primeiro, vamos calcular os valores de α, ω0 e S.
Como α > ω0, o circuito é super-amortecido. Então, teremos dois valores de S distintos:
e
Agora é só montar a equação com os valores obtidos:
Onde: Vs = 20
Passo 3
Para finalizar precisamos encontrar os valores de A1 e A2. Podemos fazer isso igualando os valores de v(0-) e v(0+):
Sabemos que:
Ou
Então:
Passo 4
Agora é só correr para o abraço!
Substituindo (1) em (2), chegaremos ao seguinte resultado:
Ou
e
Substituindo A1 e A2 em v(t) encontramos o resultado.