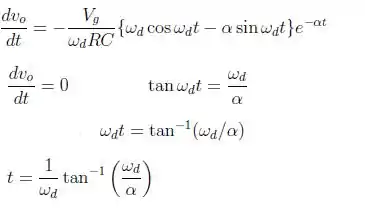Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 55
A chave do circuito mostrado na Figura P8.55 esteve fechada por um longo tempo antes de ser aberta em t = 0. Admita que os parâmetros de circuito sejam tais que a resposta seja subamortecida.
a) Deduza a expressão para vo(t) em função de vg, a, vd, C e R para t > 0.
b) Deduza a expressão para o valor de t quando a amplitude de vo for máxima.
Passo 1
Fala meu povo, tudo belezinha? Para o item a), seja a corrente na direção da queda de tensão de . Então por hipótese:
Portanto:
Ou seja,
Passo 2
Considerando ainda a corrente sobre a tensão no instante:
Logo,
Por fim, pra encontrarmos vo(t) temos:
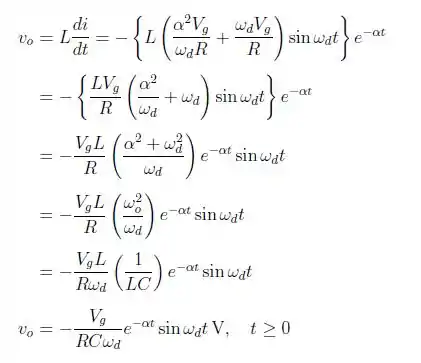
Passo 3
No item b), deduzindo a expressão, temos:
Resposta
Exercícios de Livros Relacionados
No circuito da Figura 8.104 , a chave se encontra na posição 1 há um longo tempo, porém, muda para a posição 2 em t = 0 . v 0 + , d v 0 + d t v t para t ≥ 0 .
Para o circuito da Figura 8.101 , detemrine v ( t ) para t0 . Suponha v 0 + = 4V e i 0 + = 2A .
Para o circuito do problema 8.5 , determine i e v pata t0 .
Se a chave na figura 8.103 se encontrar desligada há um longo tempo antes de t = 0 , porém é aberta em t = 0 , determine:A equação característica do circuito. i X e v R para t0 .
Obtenha i_1 e i_2 para t0 no circuito da Figura 8.106 .