Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 32
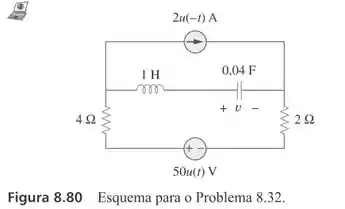
Para o circuito da Figura 8.80, determine v(t) para t > 0.
Passo 1
Como diria Jack, o estripador: vamos por partes.
Para t = 0-, o circuito equivalente é o seguinte:
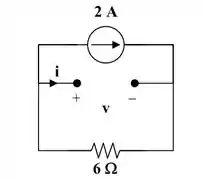
Como iremos analisar esse ramo onde o circuito está aberto, teremos que:
Passo 2
Para t > 0, teremos um circuito RLC série. Então, precisamos encontrar os valores de α, ω0 e S.
Passo 3
Como α
Onde Vf é a tensão final no capacitor, ou seja, 50V. O que nos deixa com a equação assim:
Agora é só encontrar os valores de A e B.
Passo 4
Vamos encontrar primeiro o valor de A.
Fazendo t = 0, eliminaremos boa parte da equação e poderemos utilizar os valores calculados no início da questão. Então:
Passo 5
Beleza! Agora só falta o valor de B.
No início da nossa resolução encontramos que i(0) = 0. Nós podemos usar isso na seguinte relação para encontrar o valor de B:
Mas nós sabemos que o valor da capacitância não é zero, então vamos derivar a equação de v(t) e depois aplicar ela em t = 0: