Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 65

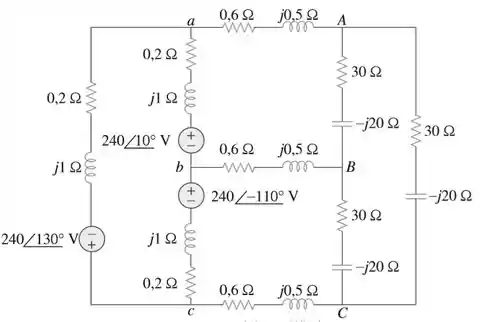
Um circuito trifásico equilibrado é mostrado na Figura 12.70. Use o PSpice ou MultiSim para determinar as correntes de linha I a A ,   I b B   e   I c C .

Passo 1

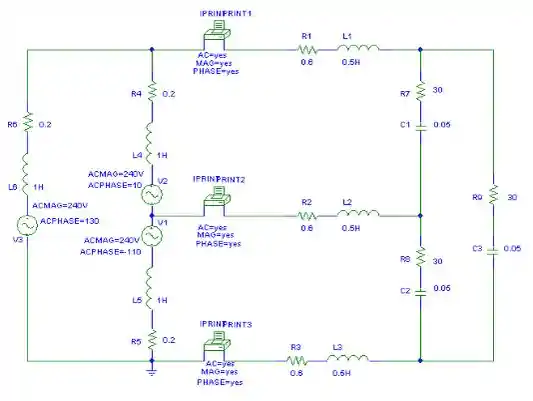
Devido à fonte conectada em delta, seguimos o Exemplo 12.12. Digitamos Pts totais = 1, Freq inicial = 0,1592 e Freq final = 0,1592. O esquema é mostrado abaixo. Depois que ele é salvo e simulado, obtemos um arquivo de saída que inclui

Passo 2

Disso podemos obter:

I a A = 11.92 ∠ 12 °   A ,     I b B = 11.02 ∠ - 108 °   A ,     I c C = 11.02 ∠ 132 °   A

Passo 3

Como este é um circuito balanceado, podemos realizar uma verificação rápida. A resistência da carga é grande em comparação com as impedâncias da linha e da fonte, portanto as ignoraremos (embora não seja difícil incluí-las). Convertendo as fontes para uma configuração Y :

V a n = 138.56 ∠ - 20 °   V r m s

Z Y = 10 - j 6.667 = 12.019 ∠ - 33.69 °

Agora temos que calcular:

I a A = 138.56 ∠ - 20 12.019 ∠ - 33.69 ° = 11.528 ∠ 13.69 ° A

Claramente, temos uma boa aproximação muito próxima do que realmente temos.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As tensões linha-linha em uma carga conectada em estrela têm magnitude igual a 440V e estão na sequência positiva em 60H z . Se as cargas estiverem equilibradas com Z 1=Z 2=Z 3= 25 ∠30 ° , determine t
Uma fonte conectada em triângulo fornece energia para uma carga conectada em estrela em um sistema trifásico equilibrado. Dado que a impedância de linha é 2+j 1Ω por fase, enquanto a impedância de car
Um sistema trifásico estrela-triângulo equilibrado possui V a n = 240 ∠0 °VR M S eZ Δ = 51–j 45Ω . Se a impedância de linha por fase for 0,4+j 1,2Ω , determine a potência complexa total para a carga.
Considere a Figura 12.55 e elabore um problema para ajudar outros estudantes a entender melhor fontes em delta equilibradas que alimentam cargas em estrela equilibradas.
Na Figura 12.56, o valor RMS da tensão de linha é 208 V. Determine a potência média liberada para a carga.