Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 62
Encontre a resposta para no circuito da figura . Seja e .
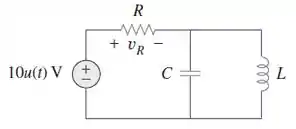
Passo 1
Pessoal, para não temos nossa fonte de tensão funcionando e o circuito está em regime permanente. Assim, o capacitor se comporta como um circuito aberto e o indutor como um curto-circuito. Dessa maneira, podemos inferir que
Como a corrente no indutor e a tensão no capacitor não podem mudar instantaneamente,
Passo 2
Quando , a fonte de tensão passa a fornecer uma tensão . Quando o tempo tende ao infinito, o circuito atinge o regime permanente, onde o capacitor se comporta como um circuito aberto e o indutor como um curto-circuito. Assim, podemos calcular o valor da corrente :
Aplicando a lei das malhas para a malha esquerda, temos:
Para obtermos a resposta transiente para , vamos desligar a fonte de tensão.
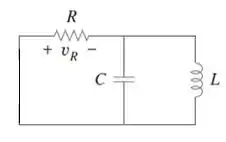
Aplicando a lei dos nós para o nó acima do capacitor, temos:
Passo 3
Aplicando a lei das malhas para a malha da esquerda,
Substituindo em :
Derivando a equação em relação a :
Dividindo a equação por ,
Substituindo os valores de e :
Passo 4
A partir da equação, conseguimos extrair a equação característica do circuito:
As raízes são:
Assim, é dada por:
Em regime permanente, . Logo,
Para
A corrente do capacitor é dada por:
Para ,
Derivando a equação , temos:
Pata ,
Logo, a equação da tensão no capacitor é:
Passo 5
A tensão no resistor pode ser encontrada aplicando a lei das malhas na malha da esquerda!
Resposta
A tensão é igual a