Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 11
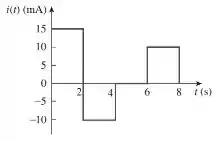
Um capacitor de 4mF tem a forma de onda para corrente apresentada na figura abaixo. Supondo que a tensão inicial é 10V, esboce a forma de onda da tensão v(t).
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para achar a tensão em relação à corrente em um capacitor. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Nosso primeiro passo vai ser analisar os trechos do gráfico. Podemos escrever como:
Ok, agora o nosso problema vai ser relembrar qual a relação que nos dá a corrente de um capacitor. Lembrou?? Não?! Dá um pulo lá em Física 3 rapidinho que eu te espero... Já voltou?? Então, me conta aii qual é a fórmula... Acertou, misêrávi!!
Mas, como queremos descobrir a tensão, vamos transformar para a notação integral.
Como ele nos deu a relação para a corrente e o valor de C, agora é só jogar os valores ali.
Passo 3
Pronto!! Agora é só jogar daqui pra lá e de lá pra cá!!