Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 57
Se a chave na figura se encontrar desligada há um longo tempo antes de , porém é aberta em , determine:
- A equação característica do circuito.
- e para .
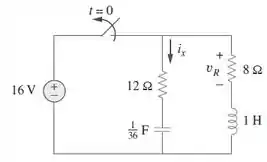
Passo 1
Galerinha, na letra (a) queremos a equação característica do circuito. Bom, seja a tensão no capacitor e a corrente no indutor. No tempo , a chave está fechada e o circuito em regime permanente, logo o capacitor se comporta como circuito aberto e o indutor como um fio. Portanto,
Passo 2
Quando , o momento seguinte a abertura da chave, nós continuamos a ter e . Agora, nós temos um circuito RLC sem fontes.
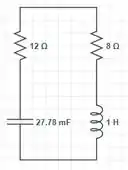
A resistência equivalente aqui é igual a:
Vamos calcular e agora, para podermos escrever nossa equação característica!
Como , nós temos um amortecimento supercrítico. Assim, as raízes da equação característica são:
Portanto, a equação característica é:
Passo 3
A letra (b) queremos achar os valores de e . Uma vez que temos as raízes da equação característica, podemos escrever a equação da corrente:
Com , temos que . Para encontrarmos , vamos olhar para o circuito abaixo no instante .
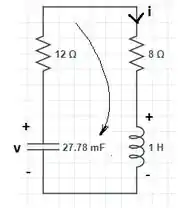
A tensão no indutor pode ser escrita como . Reorganizando a expressão,
Se derivarmos a equação da corrente , temos:
Em ,
Ficamos com um sisteminha tranquilo de resolver, de duas equações e duas incógnitas!
Por fim, as equações da corrente e da tensão podem ser escritas como:
Resposta
- ;
- e