Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 22

C a l c u l e o v a l o r e f i c a z d a c o r r e n t e e m r e g i m e p e r m a n e n t e e m R .

Passo 1

E aí gurizada tudo belezinha? Partiu calcular o valor eficaz da corrente em regime permanente em R. Vem comigo :)

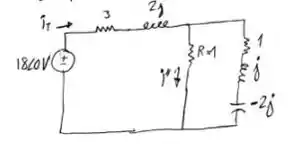
Em geral, esse regime é atingido após a passagem de um tempo suficiente para que as respostas transitórias do circuito desapareçam, vamos trazer o circuito do enunciado para cá

i^' = (8.3)/(4) = 6 A

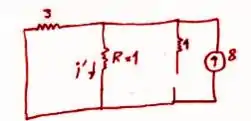
Passo 2

PAra omega = 4 Aplicando-se as relações constitutivas do indutor e do resistor (lei de Ohm)

z^' = (1 ( 1 - j ))/(2 - j) = 0,6 - 0,2 j

z e q = 3 + 2 j + z^' = 3,6 + 1,8 j

i_T = (18)/(z_e q) = (18)/(3,6 + 1,8 j) = 4 - 2 j

i^(' ') = (i_T * ( 1 - j ))/(2 - overset(˙)(j)) = 2 - 2 j = 2 sqrt(2) L - 45^@

i_R M S = sqrt((1)/(T) int_0^T 6^2 d f + (( 2 sqrt(2) )^2)/(2)) = sqrt(36 + 4) = sqrt(40) = 2 sqrt(10) A

Resposta

2 sqrt(10) A

Exercícios de Livros Relacionados

Calcule a leitura do wattímetro.
Calcule a leitura do wattímetro.
Calcule a leitura do wattímetro.
Dado i = i 1 + i 2 , onde i 1 = I 1 m cos ⁡ w 1 t i 2 = I 2 m cos ⁡ w 2 t É a corrente que flui no resistor R . Usando a definição do problema 12.13 , mostre, para w 1 ≠ w 2 , que P = P 1 + P 2 Onde P
Calcule o valor eficaz de uma corrente periódica para a qual um cicio e dado por:a) i = 3 tA 0 ≤ t ≤ 2 s 0 = 2t ≤ 4 s b) i = 6A0t2 s 0 = 2t8 s c) i = I m sin ⁡ 2 π t T A 0tT 2 0 = T 2tT s d) i = I m s