Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.10 - Ex. 1

Na Fig. 7.17, considere C1 = 1/2 F, C2 = 1F, v1(0-) = 10 V, v2(0-) = 4 V, e caIcule v1(0+), v2(0+), e a energia total armazenada no circuito em t = 0- e em t = 0+.

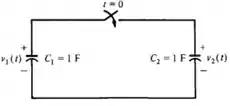
Passo 1

Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrar as tensões e a energia armazenada em determinado tempo. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??

Ok, agora o nosso problema vai ser relembrar qual a fórmula da energia armazenada em um capacitor. Responde Aí!! Lembrou?? Não?!

w c =   1 2   ∙ C ∙ v 2 ( t )

Bora lembrar da relação de tensão e corrente em um capacitor.

Essa relação é

i = C d v ( t ) d t

Passo 2

Bora então resolver isso!!

A expressão da corrente no nó generalizado acima envolvendo a chave é dada por

C 1 d v 1 d t + C 2 d v 2 d t = 0  

integrando de t = 0 + até t = 0 + da

∫ 0 - 0 + ( C 1 ∙   d v 1 + C 2   ∙ d v 2 ) = C 1   v 1 0 + - v 1 0 - + C 2 [ v 2 0 + - v 2 0 - ]

Substituindo os dados do enunciado

1 2   ∙ v 1 0 + + v 2 0 + = 9

Para t > 0, vemos que v 1 = v 2 , e então

v 1 0 + = v 2 0 +

Que assim

v 1 0 + = v 2 0 + =   6   V

Passo 3

Vamos para o último passo!!

A energia armazenada antes do fechamento da chave é

w 1 0 - =   1 2   ∙ C 1   ∙ v 1 2 0 - = 25   J

w 2 0 - =   1 2   ∙ C 2 ∙   v 2 2 0 - = 8   J

Então, a energia total será

w 0 - = w 1 0 - + w 2 0 - = 33   J

A energia armazenada após o fechamento da chave é

w 1 0 + =   1 2   ∙ C 1 ∙   v 1 2 0 + = 9   J

w 2 0 + =   1 2   ∙ C 2 ∙   v 2 2 0 + = 18   J

Então, a energia total será

w 0 + = w 1 0 + + w 2 0 + = 27   J

Prontinho!!

Resposta

v 1 0 + = v 2 0 + =   6   V

w 0 - = 33   J

w 0 + = 27   J

Exercícios de Livros Relacionados

Uma tensão CC de 10V é aplicada a um integrador com R = 50 k Ω , C = 100 μ F em t = 0 . Quanto tempo levará para o amplificador operacional saturar se as tensões de saturação forem + 12 V e - 12 V ? S
Projete um circuito para computador analógico para resolver a seguinte equação diferencial ordinária d y t d t + 4 ⋅ y t = f t Onde y 0 = 1 V .
Uma forma de onda de tensão tem as seguintes características: uma inclinação positiva de 20 V / s por 5 m s seguida por uma inclinação negativa de 10 V / s por 10 m s . Se a forma de onda for aplicada
Projete um computador analógico para simular d 2 v 0 d t 2 + 2 ⋅ d v 0 d t + v 0 = 10 ⋅ s e n2 t Onde v 0 0 = 2ev 0 ' 0 = 0 .
Um motor elétrico pode ser modelado com uma associação em série entre um resistor de 12 Ω e um indutor de 200 m H . Se uma corrente de i t = 2 t e - 10 tA passa através da associação em série, determi