Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 30
Na Figura 12.56, o valor RMS da tensão de linha é 208 V. Determine a potência média liberada para a carga.
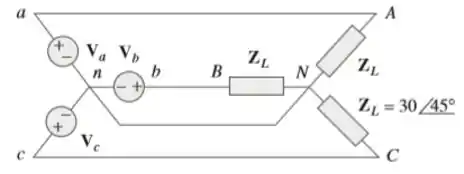
Passo 1
Questão bem de boas pessoal, atenção hein! De cara, temos que esse é um sistema balanceado, logo nós podemos substituir por um equivalente monofásico! Isso segue na figura abaixo!
Passo 2
Daqui, a potencia fica fácil de calcular! Temos que:
Mas isso é a potencia aparente. Para potência ativa, temos que:
Resposta
Exercícios de Livros Relacionados
No sistema Y - A do Prob. 13.17, a tensão da fonte, V a n = 100 / 0 ∘ V (eficazes) e Z p = 10 / 60 ∘ Ω . Calcule a tensão de linha, a corrente de linha, os módulos da corrente da carga e a potência en
C a l c u l eac o r r e n t ed el i n aI L
Para o sistema Y - Δ do Prob. 13.17 , Z p = 4 + β Ω e a potência entregue à carga e 19,2k W . Calcule a corrente de linha I L e as tensōes de fase da fonte, se V e n for tomada como referência.
Calcule a potência entregue à carga, se o módulo das tensões da fonte é 120V (eficazes) e Z p = 6 + j 9 Ω
Encontre as leituras dos wattímetros