Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 24
Uma fonte conectada em triângulo equilibrada tem tensão de fase = e uma sequência de fases positiva. Se esta for conectada a uma carga em triângulo equilibrada, determine as correntes de linha e de fase. Adote como impedância de carga por fase e impedância de linha por fase .
Passo 1
De boas pessoal, vamo pra cima! Vamos primeiro converter as fontes para o equivalente em estrela deles!
Agora fazemos uma analise por fase:
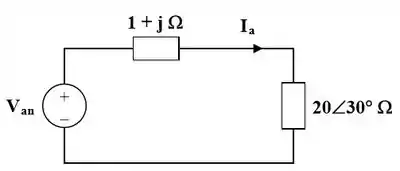
Passo 2
Mas, para achar as correntes de linha, temos que:
Resposta
Exercícios de Livros Relacionados
Obtenha as correntes de linha no circuito trifásico da Figura 12.42 .
Um sistema quadrifilar estrela-estrela equilibrado apresenta as seguintes tensões de fase V a n = 120 ∠ 0 ° ,V b n = 120 ∠ - 120 ° ,V c n = 120 ∠ 120 ° A impedância de carga por fase é 19 + j 13Ω e a
Considere a Figura 12.41 e elabore um problema para ajudar outros estudantes a entender melhor a conexão estrela-estrela equilibrada.
Para o circuito da Figura 12.43 , determine a corrente na linha neutra.
Em um sistema trifásico estrela-estrela equilibrado, a fonte é uma sequência a b c de tensões e V a n = 100 ∠ 20 °V r m s . A impedância de linha por fase é 0,6 + 1,2 jΩ , enquanto a impedância por fa