Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 83
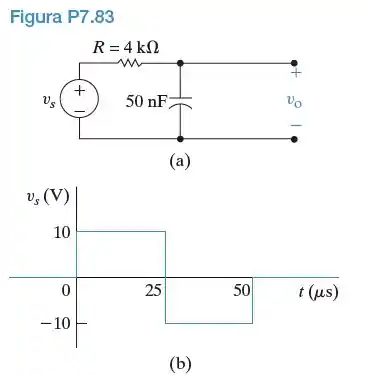
A fonte de tensão no circuito da Figura P7.83(a) está gerando o sinal mostrado na Figura P7.83(b). Não há nenhuma energia armazenada em t=0.
- Determine as expressões para que sejam válidas para os intervalos .
- Faça um gráfico de nos mesmos eixos coordenados.
- Repita (a) e (b) com R reduzido a 800 .
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre resposta de circuitos RL e RC de primeira ordem!
- Para o primeiro intervalo, temos que:
- Basta usarmos as soluções acima para criar as coordenadas e o seguinte gráfico que responde o solicitado:
- E usando os conhecimentos do primeiro item, podemos concluir para o pedido:
Nos levando ao período de:
Ou seja:
Para mais um intervalo, temos que:
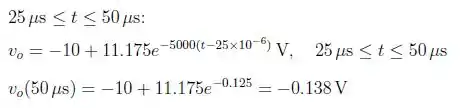
No ultimo intervalo, teremos:
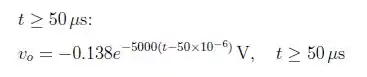
Passo 2
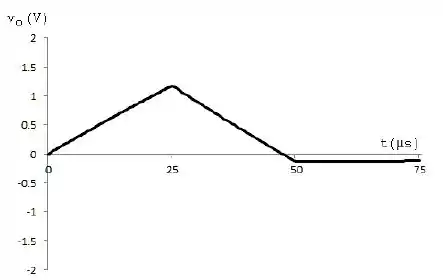
Similarmente ao item (a), temos que:
E ao item (b) temos que:
Resposta
Exercícios de Livros Relacionados
Usando funções degrau unitário escreva uma expressão para a corrente i ( t ) que satisfaça: i t = 0 ,t0 = - 10m A ,t0 i t = 0 ,t1s = 2A ,1t5s = 0 ,t5s i t = 0 , t0 = - 2A ,10t20m s = 4A ,20t40m s = 0
Esboce a tensão dada por:v (t) = t u (t) - 2 (t - 1) u (t - 1) + (t - 2) u (t - 2) v
Calcule vs ev g = 5 e - t u t V e não existe energia inicial armazenada. (Este circuita é como o integrador da figura 8.24, exceto que o capacitor tem um resistor em paralelo com ele, tornando-o um ca
CaIcule i no Ex. 8.8.1, se i_g = 10 [u (t) - u (t - 1)] A
Calcule as respostas ao degrau i e v [ i_g = u (t) A ] .