Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas Abrangentes - Ex. 79

Um gerador trifásico equilibrado tem uma sequência de fase abc com tensão de fase V a n = 255   ∠ 0 °   V . O gerador alimenta um motor de indução que pode ser representado por uma carga conectada em estrela equilibrada com impedância 12   +   j 5   Ω por fase. Determine as correntes de linha e tensões de carga por fase. Suponha uma impedância de linha de 2   Ω por fase.

Passo 1

Certo pessoal, vamos lá! Como o circuito está equilibrado, vamos fazer uma análise monofásica!

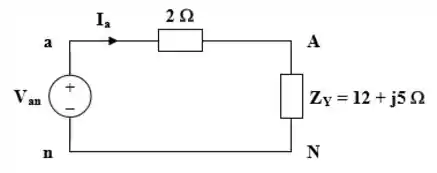
A partir dela, podemos perceber de maneira bem simples, que:

I a = V a n Z Y + 2 = 255 ∠ 0 ° 14 + 5 j = 17.15 ∠ - 19.65 ° A

Passo 2

Portanto, vamos defasar as correntes e achar o que nos queremos!

I b = I a ∠ - 120 ° = 17.15 ∠ - 139.65 °   A

I c = I a ∠ 120 ° = 17.15 ∠ 100.35 °   A

V A N = I a Z Y = 17.15 ∠ - 19.65 ° 13 ∠ 22.62 ° = 223 ∠ 2.97 ° V

Agora defasamos a tensão de fase novamente!

V B N = V A N ∠ - 120 ° = 223 ∠ - 117.63 ° V

V C N = V A N ∠ 120 ° = 223 ∠ 122.97 ° V

Resposta

I a = 17.15 ∠ - 19.65 ° A

I b = 17.15 ∠ - 139.65 °   A

I c = 17.15 ∠ 100.35 °   A

V A N = 223 ∠ 2.97 ° V

V B N = 223 ∠ - 117.63 ° V

V C N = 223 ∠ 122.97 ° V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

C a l c u l eac o r r e n t ed el i n aI L
Para o sistema Y - Δ do Prob. 13.17 , Z p = 4 + β Ω e a potência entregue à carga e 19,2k W . Calcule a corrente de linha I L e as tensōes de fase da fonte, se V e n for tomada como referência.
Calcule a potência entregue à carga, se o módulo das tensões da fonte é 120V (eficazes) e Z p = 6 + j 9 Ω
Encontre as leituras dos wattímetros
No sistema da Fig, as tensões de linha sāo um conjunto equilibrado, de seqüência positiva, com V a b = 20000 ∘ V (eficazes) e Z 1 = Z 2 = Z 3 = 10 30 ° Ω . Calcule a potência entregue a carga (a) por