58. A lâmpada de NA figura é de . Calcule para que a lâmpada opere nas condições estabelecidas.
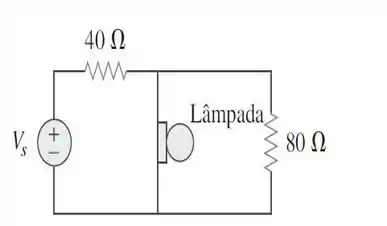
Passo 1
Olha só! A resistência de um componente, como o caso da nossa lâmpada, é dada pela divisão da tensão,, ao quadrado pela potência dele.
Sendo assim, a resistência da lâmpada é dada por:
E para achar a corrente que deve circular na lâmpada para que ela opere nas condições estabelecidas, basta dividir a tensão característica dela pela resistência que acabamos de achar:
Passo 2
Só que a lâmpada e aquela resistência de estão em paralelo. Isso significa que a resistência de também está submetida a uma fonte de tensão de , de modo que a corrente que circula nessa resistência é dada por:
Passo 3
Agora vamos esboçar o circuito pra entender o que está acontecendo. Consideremos a lâmpada como uma resistência.
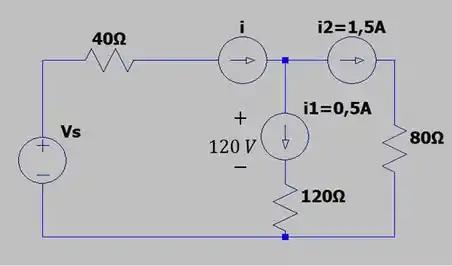
Dessa figura, tiramos que a corrente é dada por:
Assim que essa corrente passa pela resistência de , ocorre uma queda de potencial até chegar ao valor de . Sendo assim, podemos estabelecer a seguinte relação:
Essa é a tensão procurada!