Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 59
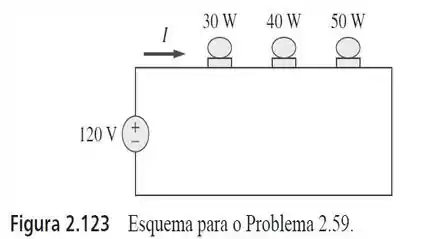
59. Três lâmpadas estão conectadas em série a uma fonte de , conforme mostrado na Figura . Determine a corrente que passa pelas lâmpadas. Cada lâmpada é específica para . Qual o valor da potência dissipada em cada lâmpada? Elas produzem muita luz?
Passo 1
Bom! A primeira coisa que temos de fazer é descobrir o valor da resistência para cada lâmpada. Para isso bastar usar a relação abaixo:
A resistência é dada pela divisão do quadrado da tensão pela potência específica de cada lâmpada.
Sendo assim, obtemos as seguintes resistências...
Como as três lâmpadas estão em série, a resistência equivalente é dada por:
Passo 2
E agora, dado que é um circuito em série, para encontrar a corrente circulante, basta dividir a fonte de tensão pela resistência total equivalente que já encontramos:
A questão nos pede para determinar também a potência em cada lâmpada, né não?
Ora bolas! Para fazer isso, basta saber que a potência é dada pelo produto da resistência pela corrente circulante ao quadrado, que no caso, por ser um circuito com lâmpadas em série; tem sempre o mesmo valor.
Desse jeito, utilizando as fórmulas abaixo:
Obtemos os seguintes resultados:
Claramente esses valores estão bem abaixo das potências nominais de cada lâmpada, portanto, não esperaríamos muita luz de nenhuma delas. Para funcionar corretamente, eles precisam estar conectados em paralelo.