Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 61
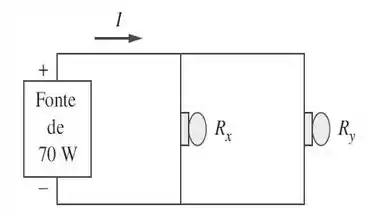
61. Como engenheiro de projetos lhe foi solicitado projetar um sistema de iluminação formado por uma fonte de alimentação de e duas lâmpadas, conforme mostrado na Figura 2.124. Você deve selecionar as duas lâmpadas das três opções a seguir.
, custo (tamanho padrão)
, custo (tamanho padrão)
, custo (tamanho não-padronizado)
O sistema deve ser projetado para um custo mínimo de modo que
Passo 1
Bom! Quando se foi falado que o sistema deve ser projetado para um custo mínimo de modo que significa dizer que ele deve ser projetado com:
Com dentro do seguinte intervalo:
Como só podemos escolher duas resistências, e temos três disponíveis; o melhor jeito de se resolver esta questão é testar as combinações e ver qual é mais satisfatória.
Bora começar então, com e :
A resistência de está em paralelo com a de , de modo que a resistência equivalente para essa associação vai ser igual a:
E para achar a corrente total circulante nesse caso, basta usar a seguinte relação, sendo a potência fornecida, de :
Já que precisa ser menor que , essa corrente que obtivemos é inaceitável.
E quanto ao custo; já que pegamos e :
Gastamos !
Passo 2
Vamos pegar agora, e :
A resistência de está em paralelo com a de , de modo que a resistência equivalente para essa associação vai ser igual a:
E para achar a corrente total circulante nesse caso, basta usar a seguinte relação, sendo a potência fornecida, de :
Essa corrente sim, é aceitável.
E quanto ao custo; já que pegamos e :
Gastamos !
Passo 3
E por último, testemos e :
A resistência de está em paralelo com a de , de modo que a resistência equivalente para essa associação vai ser igual a:
E para achar a corrente total circulante nesse caso, basta usar a seguinte relação, sendo a potência fornecida, de :
Essa corrente também é aceitável.
E quanto ao custo; já que pegamos e :
Gastamos !
Passo 4
As associações e e também e satisfazem a condição imposta pela corrente, estando dentro do intervalo permitido. Entretanto, o primeiro tem um custo menor e por isso é o vencedor dessa batalha! Palmas pra ele!
Resposta
e .