Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 11.Problemas - Ex. 35

Uma linha trifásica tem uma impedância de 0,1 + j0,8 Ω / ϕ . A linha alimenta duas cargas

trifásicas equilibradas ligadas em paralelo. A primeira carga está absorvendo um total de

630 kW e de 840 kVAR. A segunda carga está ligada em Y e tem uma impedância de 15,36

- j4,48 Ω / ϕ . A tensão fase-neutro na carga é 4.000 V. Qual é o módulo da tensão de linha

no início dela?

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe circuitos trifásicos equilibrados!

Podemos ilustrar o sistema da seguinte forma:

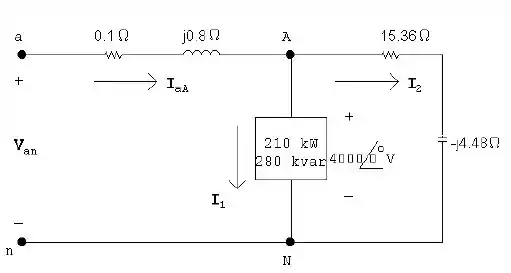
Sabemos que:

4000 I 1 * = 210 + j 280 10 3 → I 1 * = 52,5 + j 70 A

Logo:

I 1 = 52,5 - j 70 A

Passo 2

Determinando a outra corrente:

I 2 = 4000 / 0 ° 15,36 - j 4,48 = 240 + j 70 A

Logo a soma:

I a A = I 1 + I 2 = 292,5 + j 0 A

Feito isso, para a tensão an temos:

V a n = 4000 + j 0 + 292,5 ( 0,1 + j 0,8 )

E por fim,

V a b = 3 V a n = 6990,62 V

Resposta

V a b = 6990,62 V

Exercícios de Livros Relacionados

Para o circuito da Figura 12.43 , determine a corrente na linha neutra.
Em um sistema trifásico estrela-estrela equilibrado, a fonte é uma sequência a b c de tensões e V a n = 100 ∠ 20 °V r m s . A impedância de linha por fase é 0,6 + 1,2 jΩ , enquanto a impedância por fa
Considere a Figura 12.45 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos com conexão estrela-triângulo.
No sistema trifásico estrela-triângulo equilibrado da Figura 12.46 , determine a corrente de linha I L e a potência média liberada para a carga.
No sistema estrela-triângulo mostrado na Figura 12.44 , a fonte é uma sequência positiva com V a n = 240 ∠ 0 °V e impedância por fase Z p = 2 - j 3Ω . Calcule a tensão de linha V L e a corrente da lin