Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 10
Para o circuito da Figura , determine a corrente na linha neutra.
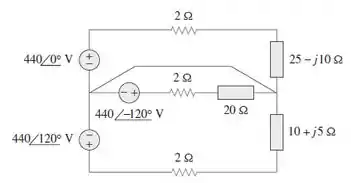
Passo 1
Nós temos um sistema estrela-estrela, o que já implica em termos correntes de linhas iguais as correntes de fase. Já temos em mãos as tensões de fase e as impedâncias de linha e fase. Portanto, para calcular a corrente, basta dividirmos a tensão pela soma das impedâncias! Antes de tudo, vamos passar a impedância da fase para forma polar:
Agora, passando a impedância da fase para a forma polar:
Por último, passando a impedância da fase para a forma polar:
Passo 2
Portanto, a corrente de linha será igual:
A corrente que passa pelo condutor neutro, pela lei e Kirchhoff, é dada por:
Substituindo os valores na equação, temos:
Resposta
As correntes de linha são iguais a:
A corrente no neutro é igual a:
Exercícios de Livros Relacionados
8-Determine o valor eficaz de Io no circuito trifásico não equilibrado da Figura P11.8. Figura P11.8.
7-a) Determine Io no circuito da Figura P11.7. b) Determine VAN. c) Determine VAB. d) O circuito é ou não um sistema trifásico equilibrado?Figura P11.7
12-O módulo da tensão de fase de uma fonte trifásica ideal, equilibrada, ligada em Y, é 125 V. A fonte está ligada a uma carga equilibrada, ligada em Y, por uma linha de distribuição que tem uma imped
Calcule a potência complexa em cada fase da carga não equilibrada do Problema 11.20.
A tensão fase-neutro no circuito da Figura P11.43 é 680 V, a sequência de fases é positivae a impedância de carga é 16 - j12 Ω / ϕ .a) Determine a leitura do wattímetro.b) Determine a potência reativa