Em um sistema trifásico estrela-estrela equilibrado, a fonte é uma sequência a b c de tensões e V a n = 100 ∠ 20 °V r m s . A impedância de linha por fase é 0,6 + 1,2 jΩ , enquanto a impedância por fase da carga é 10 + j 14Ω . Calcule as correntes de linha e as tensões de carga.

As correntes de linha são iguais a: I a = 5,396 ∠ - 35,11 °A I b = 5,396 ∠ - 155,11 °A I c = 5,396 ∠ 84,89 °A As tensões nas cargas são iguais a: V c a r g a - a = 92,84 ∠ 19,35 °V V c a r g a - b = 92 , 84 ∠ - 100,65 °V V c a r g a - c = 9 2 , 84 ∠ 139,35 °V

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 8

Em um sistema trifásico estrela-estrela equilibrado, a fonte é uma sequência de tensões e . A impedância de linha por fase é , enquanto a impedância por fase da carga é . Calcule as correntes de linha e as tensões de carga.

Passo 1

Galera, a fonte de tensão é da sequência . Portanto, podemos escrever as demais tensões de fase da seguinte forma:

Passo 2

Podemos desenhar a o circuito monofásico da seguinte forma:

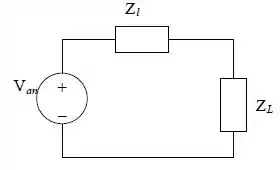
Podemos escrever a corrente de linha da seguinte forma:

Para efetuarmos essa conta, precisamos passar para a forma polar a soma das impedâncias de linha e carga:

Assim, as correntes de linha são iguais a:

Passo 3

Por fim, para encontrarmos a tensão na carga, basta multiplicarmos a impedância pela corrente de fase/linha.

Passando a impedância para a forma polar:

Assim,

Logo, a tensão é igual a:

Resposta

As correntes de linha são iguais a:

As tensões nas cargas são iguais a:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As leituras dos wattímetros no circuito da Figura 11.20 são as seguintes: W1 = 40.823,09W e W2 = 103.176,91 W. O módulo da tensão de linha é 2.400 3 V. A sequência de fasesé positiva. Determine Z ϕ .

Deduza as equações 11.56 e 11.57.

a) Calcule a potência complexa associada a cada fase da carga equilibrada no Problema 11.19.b) Se o método de dois wattímetros for utilizado para medir a potência média fornecida à carga, especifique

Um banco de capacitores equilibrados em ∆ está ligado em paralelo com a carga descritano Problema para avaliação 11.9. Isso é equivalente a colocar um capacitor em paralelocom a carga em cada fase. As